Problema
(Indicado a partir do 9º ano do E. F.)
(Revista Tzaloa, ano 1, número 3- 2009) Na figura abaixo, sejam [tex]CA = 2[/tex], [tex]CB = 3[/tex], [tex]\angle CAP=\angle PBC=90^{\circ}[/tex] e [tex]\angle APB=60^{\circ}[/tex].
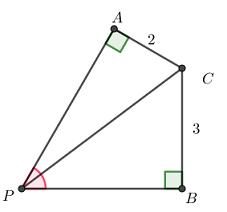
Encontre a medida do segmento [tex]\overline{PC}[/tex].

Notações e lembretes
✐ A soma das medidas dos ângulos internos de qualquer triângulo é [tex]180^\circ.[/tex]
Notações:
– Denotaremos a medida do ângulo de vértice [tex]V[/tex] e definido por dois pontos, digamos [tex]X [/tex] e [tex]Y[/tex], por [tex]\angle XVY. [/tex]
– Denotaremos o segmento definido por dois pontos, digamos [tex]X[/tex] e [tex]Y[/tex], por [tex]\overline{XY}[/tex] e o seu comprimento por [tex]XY[/tex].
Solução
Para a solução do problema, vamos prolongar os segmentos [tex]\overline{PA}[/tex] e [tex]\overline{BC}[/tex].
Observem que esses segmentos não são paralelos (os ângulos com vértices nos pontos [tex]P[/tex] e [tex]B[/tex] têm medidas diferentes); logo, os seus prolongamentos de intersectarão em um ponto que denotaremos por [tex]D[/tex].
Como [tex]\angle APB=60^{\circ}[/tex] e [tex]\angle PBD=90^{\circ}[/tex], podemos utilizar o Lembrete e concluir que [tex]\angle PDB=30^{\circ}[/tex].
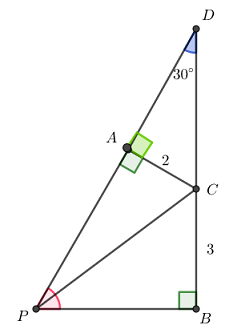
- No [tex]\triangle DAC[/tex] temos que
- Ainda no [tex]\triangle DAC[/tex] temos que
- No [tex]\triangle PBD[/tex] temos
[tex]\qquad \mbox{sen}\;30^{\circ}=\dfrac{2}{CD}\Rightarrow \dfrac{1}{2}=\dfrac{2}{CD}\Rightarrow CD=4.[/tex]
[tex]\qquad \cos \;30^{\circ}=\dfrac{AD}{CD}\Rightarrow \dfrac{\sqrt{3}}{2}=\dfrac{AD}{4}\Rightarrow AD=2\sqrt{3}.[/tex]
[tex]\qquad \mbox{tg} \;30^{\circ}=\dfrac{PB}{(BC+CD)}\Rightarrow \dfrac{\sqrt{3}}{3}=\dfrac{PB}{7}\Rightarrow PB=\dfrac{7\sqrt{3}}{3}.[/tex]
Agora, utilizando o Teorema de Pitágoras no [tex]\triangle PBC[/tex], segue que:
[tex]\qquad (PC)^2=(PB)^2+(BC)^2\\
\qquad (PC)^2=\bigg(\dfrac{7\sqrt{3}}{3}\bigg)^2+3^2\\
\qquad (PC)^2=\dfrac{49\cdot 3}{9}+9\\
\qquad (PC)^2=\dfrac{49}{3}+9\\
\qquad (PC)^2=\dfrac{76}{3}\\
\qquad PC=\pm\sqrt{\dfrac{76}{3}}[/tex]
Portanto, [tex]\, \fcolorbox{black}{#eee0e5}{$PC=\sqrt{\dfrac{76}{3}}\text{ unidades de comprimento}$}\;[/tex].
Solução elaborada pelos Moderadores do Blog.
