Problema
(Indicado a partir do 9º ano do E. F.)
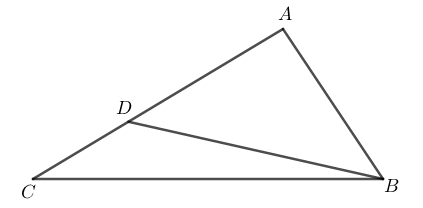
(Challenging Problems in Geometry – Adaptado) Considere o triângulo formado pelos pontos [tex]A[/tex], [tex]B[/tex] e [tex]C[/tex]. Sobre o segmento [tex]\overline{AC}[/tex] existe um ponto [tex]D[/tex] tal que [tex]AB=AD[/tex].
Sabendo que [tex] m(A\widehat{B}C)-m(A\widehat{C}B)=30^{\circ}[/tex], encontre a medida do ângulo [tex]C\widehat{B}D[/tex].

Lembrete e notações
✐ Em todo triângulo, a medida de qualquer ângulo externo é igual à soma das medidas dos dois ângulos internos não adjacentes.
Notações:
– Denotaremos a medida do ângulo de vértice [tex]V[/tex] e definido por dois pontos, digamos [tex]X [/tex] e [tex]Y[/tex], por [tex]m(X\widehat{V}Y). [/tex]
– Denotaremos o segmento definido por dois pontos, digamos [tex]X[/tex] e [tex]Y[/tex], por [tex]\overline{XY}[/tex] e o seu comprimento por [tex]XY[/tex].
Solução
Antes de mais nada, observamos que
[tex]\qquad m(C\widehat{B}D)=m(A\widehat{B}C)-m(A\widehat{B}D).\;\;\;\; \textcolor{#800000}{(i)}[/tex]
Como [tex]AB=AD[/tex] o triângulo [tex]ABD[/tex] é isósceles de base [tex]\overline{BD}[/tex], então
[tex]\qquad m(A\widehat{D}B)=m(A\widehat{B}D).\;\;\;\;\textcolor{#800000}{(ii)}[/tex]
Substituindo [tex]\textcolor{#800000}{(ii)}[/tex] em [tex]\textcolor{#800000}{(i)}[/tex] vem que:
[tex]\qquad m(C\widehat{B}D)=m(A\widehat{B}C)-m(A\widehat{D}B).\;\;\;\;\textcolor{#800000}{(iii)}[/tex]
Notemos que [tex]A\widehat{D}B[/tex] é um ângulo externo ao triângulo [tex]CBD[/tex]. Então, do Lembrete, segue que:
[tex]\qquad m(A\widehat{D}B)=m(C\widehat{B}D)+m(A\widehat{C}B).\;\;\;\;\textcolor{#800000}{(iv)}[/tex]
Substituindo [tex]\textcolor{#800000}{(iv)}[/tex] em [tex]\textcolor{#800000}{(iii)}[/tex] obtemos
[tex]\qquad m(C\widehat{B}D)=m(A\widehat{B}C)-\big(m(C\widehat{B}D)+m(A\widehat{C}B)\big)[/tex]
[tex]\qquad m(C\widehat{B}D)=m(A\widehat{B}C)-m(C\widehat{B}D)-m(A\widehat{C}B)[/tex]
[tex]\qquad 2\cdot m(C\widehat{B}D)=m(A\widehat{B}C)-m(A\widehat{C}B). [/tex]
Do enunciado sabemos que [tex]m(A\widehat{B}C)-m(A\widehat{C}B)=30^{\circ}[/tex]; portanto,
[tex]\qquad 2\cdot m(C\widehat{B}D)=30^{\circ}[/tex],
ou seja, [tex]\,\fcolorbox{black}{#eee0e5}{$m(C\widehat{B}D)=15^{\circ}$}\,[/tex].
Solução elaborada pelos Moderadores do Blog.
