Problema
(Indicado a partir do 1º ano do E. M.)
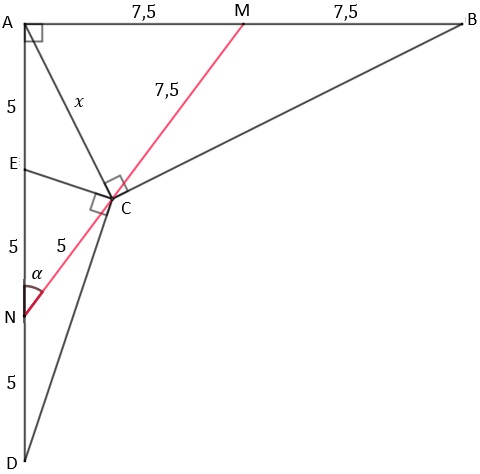
No boomerang mostrado na figura abaixo estão indicados os comprimentos [tex]AB=15[/tex], [tex]AE=5[/tex] e [tex]ED=10[/tex]. Os ângulos retos também estão destacados na figura.
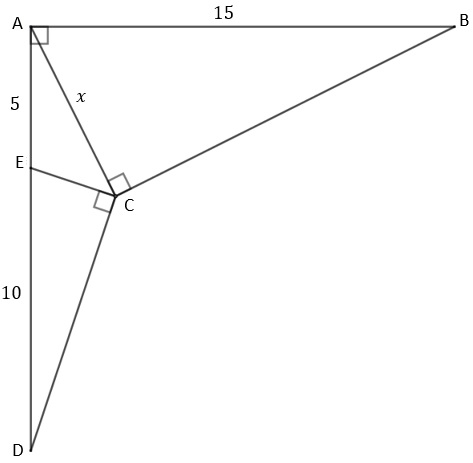
Calcule o comprimento [tex]x[/tex] do segmento [tex]\overline{AC}[/tex].

Lembretes
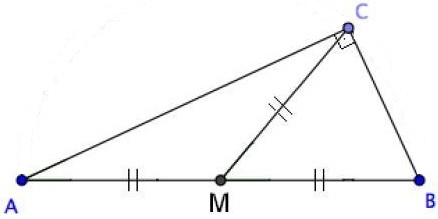
(01) A mediana de um triângulo retângulo relativa à hipotenusa mede metade da hipotenusa.
(02) Lei dos Cossenos
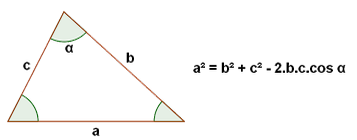
(03) Teorema de Pitágoras: Em um triângulo retângulo, o quadrado da hipotenusa é a soma dos quadrados dos catetos..
✐ Notação: Denotaremos o segmento definido por dois pontos, digamos [tex]X[/tex] e [tex]Y[/tex], por [tex]\overline{XY}[/tex] e o seu comprimento por [tex]XY[/tex].
Solução
Inicialmente, vamos construir os segmentos [tex]\overline{CM}[/tex], mediana do triângulo [tex]ACB[/tex], e [tex]\overline{CN}[/tex], mediana do triângulo [tex]CED[/tex].
Pelo Lembrete (01), temos que [tex]CM=MA=MB=7,5\,[/tex] e [tex]\,CN=EN=ND=5[/tex].
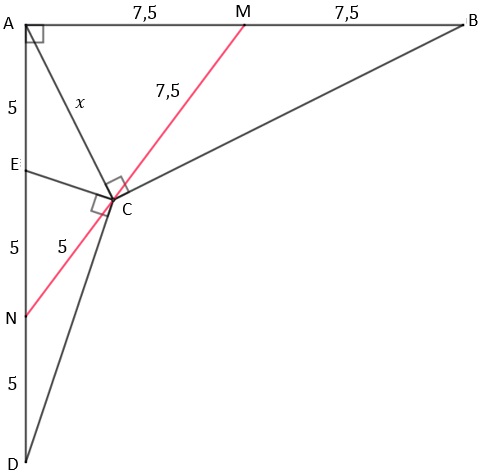
A figura anterior indica que os pontos [tex]N[/tex], [tex]C[/tex] e [tex]M[/tex] estão alinhados; e como essa é uma informação que nos ajudará na solução do problema, vamos tentar provar esse alinhamento.
Observe que se os pontos [tex]N[/tex], [tex]C[/tex] e [tex]M[/tex] estiverem de fato alinhados, então o ponto [tex]C[/tex] pertence à hipotenusa do triângulo retângulo [tex]MAN[/tex]. Para fazer tal verificação vamos, inicialmente, usar o Teorema de Pitágoras para calcular a medida do segmento [tex]\overline{MN}[/tex] (hipotenusa do triângulo retângulo):
[tex]\qquad (NM)^{2}=(AN)^{2}+(AM)^{2}\\
\qquad (NM)^{2}=10^{2}+7,5^{2}=156,25=12,5^{2}.[/tex]
Dessa forma, [tex]NM=12,5\text{ cm}[/tex].
Mas
[tex]\qquad NC+CM=5+7,5=12,5[/tex];
logo, [tex]NC+CM=NM[/tex] e, portanto, os pontos [tex]N[/tex], [tex]M[/tex] e [tex]C[/tex] são colineares.
Por outro lado, como o triângulo [tex]MAN[/tex] é retângulo, podemos descobrir o cosseno do ângulo [tex]A\hat{N}M[/tex], cuja medida denotaremos por [tex]\alpha[/tex], dividindo a medida do cateto adjacente pelo comprimento da hipotenusa (relações trigonométricas no triângulo retângulo).
Assim, [tex]cos \; \alpha =\dfrac{10}{12,5}=\dfrac{4}{5}[/tex].
Finalmente, pelo Lembrete (02), podemos aplicar a lei dos cossenos no triângulo [tex]ACN[/tex]. Dessa forma:
[tex]\qquad x^{2}=10^{2}+5^{2}-2\cdot10\cdot5\cdot cos \; \alpha[/tex]
[tex]\qquad x^{2}=100+25-2\cdot10\cdot5\cdot \dfrac{4}{5}[/tex]
[tex]\qquad x^{2}=125-80=45[/tex]
[tex]\qquad x=\pm 3\sqrt{5}[/tex].
Como [tex]x[/tex] é um comprimento, [tex]x \gt 0[/tex]; portanto, [tex]\fcolorbox{black}{#eee0e5}{$x=3\sqrt{5}$}[/tex].
Solução elaborada pelos Moderadores do Blog.
