✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Médio)
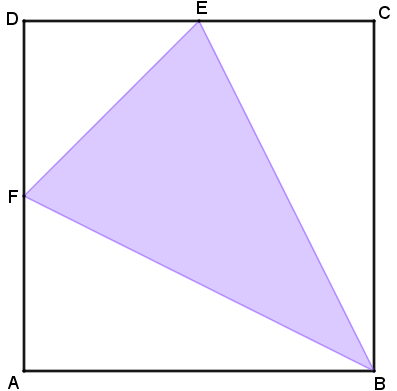
[tex] ABCD [/tex] é um quadrado cuja área mede [tex]40\,\text{cm}^2[/tex].
Sabendo que [tex]E[/tex] e [tex]F[/tex] são, respectivamente, os pontos médios dos lados [tex]\overline{CD}[/tex] e [tex]\overline{DA}[/tex], determine a área do triângulo [tex]BEF[/tex].
Solução
Para não fazer muitas contas, vamos supor que [tex]l[/tex] seja o comprimento em centímetros de cada lado do quadrado. Assim, como [tex]E[/tex] e [tex]F[/tex] são, respectivamente, os pontos médios dos lados [tex]\overline{CD}[/tex] e [tex]\overline{DA}[/tex], o comprimento em centímetros dos segmentos [tex]AF[/tex], [tex]FD[/tex], [tex]DE[/tex] e [tex]EC[/tex] é [tex]\dfrac{l}{2}\,.[/tex]
Agora, observe que a área [tex]\textcolor{#9966FF}{S}[/tex] do triângulo [tex]\textcolor{#9966FF}{BEF}[/tex] é a diferença entre a área do [tex] ABCD [/tex] e a soma das áreas dos triângulos [tex]\textcolor{#FF7F00}{BCE}[/tex], [tex]\textcolor{#0099FF}{EDF}[/tex] e [tex]\textcolor{#FF0000}{FAB}[/tex], indicadas na figura abaixo por, respectivamente, [tex]\textcolor{#FF7F00}{S_1}[/tex], [tex]\textcolor{#0099FF}{S_2}[/tex] e [tex]\textcolor{#FF0000}{S_3}[/tex].
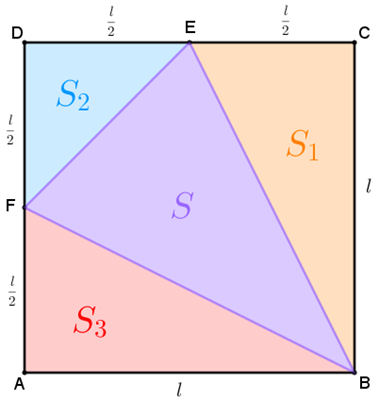
A partir dessas observações, vamos aos cálculos!
[tex] \qquad \textcolor{#9966FF}{S}=40-\left(\textcolor{#FF7F00}{S_1}+\textcolor{#0099FF}{S_2}+\textcolor{#FF0000}{S_3} \right)\\
\qquad \textcolor{#9966FF}{S}=40-\left(\textcolor{#FF7F00}{\dfrac{l\cdot \frac{l}{2}}{2}}+\textcolor{#0099FF}{\dfrac{\frac{l}{2}\cdot \frac{l}{2}}{2}}+\textcolor{#FF0000}{\dfrac{l\cdot \frac{l}{2}}{2}} \right)\\
\qquad \textcolor{#9966FF}{S}=40-\left(\textcolor{#FF7F00}{\dfrac{l^2}{4}}+\textcolor{#0099FF}{\dfrac{l^2}{8}}+\textcolor{#FF0000}{\dfrac{l^2}{4}} \right)\\
\qquad \textcolor{#9966FF}{S=40-\dfrac{5\cdot l^2}{8}}[/tex].
Como [tex]l^2[/tex] é a área do quadrado [tex] ABCD [/tex], então [tex]l^2=40[/tex] e, com isso,
[tex] \qquad \textcolor{#9966FF}{S=40-\dfrac{5 \cdot 40}{8}}[/tex]
[tex] \qquad \textcolor{#9966FF}{S=15\,\text{cm}^2}[/tex].
Portanto, a área do triângulo [tex]BEF[/tex] é [tex]\fcolorbox{black}{#eee0e5}{$15\,\text{cm}^2 $}\,[/tex].
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
