✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Muito Difícil)
(UK Junior Mathematical Olympiad, 2012) O número [tex]23173[/tex] tem duas características interessantes:
- todo par de dígitos vizinhos forma um número primo,
- todos esses números primos formados são distintos dois a dois.

Qual é o maior número natural que satisfaz essas duas condições?
Solução
Vamos ter de lidar com números primos de dois algarismos. Assim observamos, inicialmente, que nenhum primo de dois dígitos termina em [tex]5[/tex] ou em um dígito par, já que um número de dois dígitos que seja par é divisível por [tex]2[/tex] (e portanto não é primo) e um número de dois dígitos que termine em [tex]5[/tex] é divisível por [tex]5[/tex] (e igualmente não primo).
Por outro lado, observe que, para os números com os quais iremos trabalhar, todo algarismo que ocupe uma posição a partir da segunda (da esquerda para direita) será necessariamente segundo algarismo de um número primo com dois algarismos. Dessa forma, os algarismos [tex]2, 4, 6, 8[/tex] ou [tex]5[/tex] podem aparecer apenas como o primeiro dígito dos números que satisfaçam as condições do problema.
Feitas essas observações, vamos iniciar a nossa análise e para isso seja [tex]M[/tex] o maior número que satisfaz as duas condições do problema
Com exceção do primeiro dígito, os demais dígitos dos números que analisaremos são ímpares e diferentes de [tex]5[/tex]. Assim, precisaremos de números primos com dois dígitos tais que os dois dígitos sejam ímpares e diferentes de [tex]5[/tex], e existem apenas dez números primos que satisfazem essas condições: [tex]11, 13, 17, 19, 31, 37, 71, 73, 79[/tex] e [tex]97[/tex].
Para ajudar na montagem dos números que analisaremos, vamos escrever estes números em uma tabela, colocando aqueles que tenham o mesmo primeiro dígito em uma mesma linha e aqueles com o mesmo segundo dígito em uma mesma coluna.
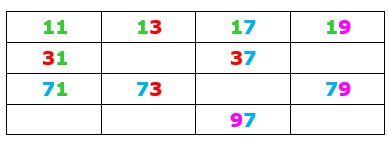
Uma condição inicial para que tenhamos o maior número dentre os que satisfazem as condições do problema é que utilizemos todos os dez primos da tabela. Vamos imaginar esses dez primos colocados um atrás do outro e imaginar os problemas que podemos encontrar:
- Todo par de dígitos vizinhos de [tex]M[/tex] é um número primo e os primos formados são dois a dois distintos. Mas observe que se escrevemos os primos [tex]11[/tex] e [tex]13[/tex] seguidamente ficamos com os dígitos [tex]1113[/tex] e teremos dois primos vizinhos iguais:
- Dois algarismos vizinhos devem formar um número primo. Observe que se escrevemos os primos [tex]19[/tex] e [tex]31[/tex] seguidamente ficamos com os dígitos [tex]1931[/tex] e teremos dois dígitos vizinhos definindo um número não primo: [tex]93[/tex], que é divisível por [tex]3[/tex].
- Agora, perceba que não podemos ter números com mais de doze dígitos satisfazendo as condições do problema.
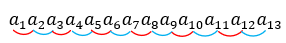
Com efeito, para que tenhamos treze dígitos satisfazendo as condições do problema devemos ter doze pares de primos vizinhos. Observe que primeiro primo pode ter o primeiro dígito par ou [tex]5[/tex] e, portanto, ser diferente dos primos mostrados na tabela. Mas os demais não; e isso implicaria em termos onze primos com dois dígitos ímpares, diferentes entre si, o que sabemos não ser possível pois os únicos primos nessas condições são os dez mostrados na tabela.

Vamos mostrar que é possível que [tex]M[/tex], o maior número que satisfaz as duas condições do problema, tenha doze dígitos. Para isso, vamos supor que podemos encontrar um número de doze algarismos cujos dígitos definam todos os dez números primos da tabela e com o primeiro dígito igual a [tex]2, 4, 6, 8[/tex] ou [tex]5[/tex], e tentar construir o maior número desse tipo.
Vamos a princípio reservar o primeiro dígito dos números que analisaremos para um dos algarismos [tex]2, 4, 6, 8[/tex] ou [tex]5[/tex] e analisar os onze outros:
[tex]\qquad \qquad\underline{\quad}\,a_2a_3a_4a_5a_6a_7a_8a_9a_{10}a_{11}a_{12}[/tex].
Observe que qualquer algarismo [tex]a[/tex] que não seja o dígito [tex]a_2[/tex] e nem o dígito [tex]a_{12}[/tex] define dois números primos sucessivos [tex]ya[/tex] e [tex]ax[/tex] com dígitos ímpares.
A partir dessa observação, concluímos que:
- os algarismos que não ocupam as posições [tex]2[/tex] e [tex]12[/tex] devem ser algarismos que aparecem na tabela uma mesma quantidade de vezes como primeiro dígito e como segundo dígito;
- o algarismo que ocupará a posição [tex]2[/tex] deve aparecer na tabela uma vez a mais como primeiro dígito;
- o algarismo que ocupará a posição [tex]12[/tex] deve aparecer na tabela uma vez a mais como segundo dígito.
Pronto, como na tabela vemos que o algarismo [tex]1[/tex] ocorre quatro vezes como primeiro dígito e apenas três vezes como segundo dígito, enquanto que o algarismo [tex]9[/tex] ocorre uma vez como primeiro dígito e duas vezes como segundo dígito, para que todos os números primos que contêm um dígito [tex]1[/tex] e um dígito [tex]9[/tex] apareçam na composição de [tex]M[/tex] , [tex]a_{2}=1[/tex] e [tex]a_{12}=9[/tex].
-
► Por enquanto o [tex]M[/tex] está com esta cara: [tex]M=a_11a_3a_4a_5a_6a_7a_8a_9a_{10}a_{11}9[/tex].
Vejamos o valor de [tex]a_1[/tex]: [tex]a_1[/tex] é par ou é cinco, o número de dois dígitos [tex]\boxed{a_11}[/tex] deve ser primo e [tex]a_1[/tex] deve ser o maior possível. Assim [tex]a_1=6[/tex] e [tex]M[/tex] fica com esta cara:
- ► [tex]M=61a_3a_4a_5a_6a_7a_8a_9a_{10}a_{11}9[/tex].
Olhando a tabela, o maior valor possível para [tex]a_3[/tex] é [tex]9 [/tex] e, com isso,
- ►[tex]M=619a_4a_5a_6a_7a_8a_9a_{10}a_{11}9[/tex].
Como o [tex]M[/tex] termina com o [tex]9[/tex], olhando a tabela vemos uma única opção para [tex]a_{11}[/tex]: [tex]7[/tex]. Veja como está o [tex]M[/tex]:
- ► [tex]M=619a_4a_5a_6a_7a_8a_9a_{10}79[/tex].
Olhando novamente a tabela, temos uma única opção para [tex]a_{4}[/tex] pois o único primo que começa com [tex]9[/tex] é o [tex]97[/tex]. Veja como está o [tex]M[/tex] e os primos não utilizados da tabela:
- ► [tex]M=6197a_5a_6a_7a_8a_9a_{10}79[/tex].
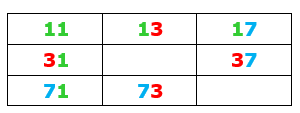
Vamos agora analisar os primos que estão na tabela e têm um dígito [tex]7[/tex]:
– Para o primo [tex]7a_5[/tex], a tabela oferece duas opções: [tex]71\,[/tex] e [tex]\,73[/tex]. Como estamos buscando o maior valor possível para [tex]M[/tex], o algarismo [tex]a_5[/tex] deve ter o maior valor possível; no nosso caso, [tex]a_5=3.[/tex]
– Para o primo [tex]a_{10}7[/tex], a tabela também nos oferece duas opções: [tex]17\,[/tex] e [tex]\,37[/tex]. Para que [tex]M[/tex] tenha o maior valor possível, algarismos maiores devem ser colocados nas posições mais à esquerda e, os menores, mais à direita. Como [tex]a_{10}[/tex] é a última posição dentre as não ocupadas, [tex]a_{10}=1.[/tex]
Agora, [tex]M[/tex] ganhou mais dois dígitos:
- ► [tex]M=61973a_6a_7a_8a_9179[/tex].
Olhando a nossa tabela, podemos continuar adicionando o maior dígito possível sempre à direita dos dígitos iniciais.
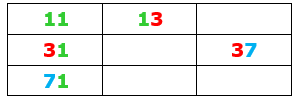
Vamos lá:
- Para [tex]a_6[/tex], temos duas possibilidades:[tex]1[/tex] ou [tex]7[/tex]; e [tex]7[/tex] é maior.
- Para [tex]a_7[/tex], temos uma única possibilidade:[tex]a_7=1[/tex] .
- Para [tex]a_8[/tex], temos duas possibilidades:[tex]1[/tex] ou [tex]3[/tex]; e [tex]3[/tex] é maior.
- Para [tex]a_9[/tex], temos uma única possibilidade:[tex]a_9=1[/tex] .
► [tex]M=619737a_7a_8a_9179[/tex].
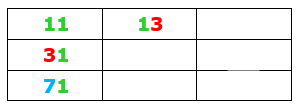
► [tex]M=6197371a_8a_9179[/tex].
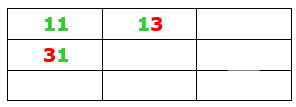
► [tex]M=61973713a_9179[/tex].

► [tex]M=619737131179[/tex].
Portanto, o maior número natural que satisfaz essas duas condições do problema é o [tex]\,\fcolorbox{black}{#eee0e5}{$619\,737\,131\,179$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
