Problema
(Indicado a partir do 9º ano do E. F.)
(Geometry Problems and Solutions From Mathematical Olympiads – Adaptado) Considere o pentágono regular [tex]ABCDE[/tex] e a estrela [tex]EBDAC[/tex] que possui área igual a [tex]1[/tex]. Sejam [tex]P[/tex] o ponto de interseção dos segmentos [tex]\overline{AD}[/tex] e [tex]\overline{BE}[/tex] e [tex]Q[/tex] o ponto de interseção dos segmentos [tex]\overline{BD}[/tex] e [tex]\overline{CE}[/tex].
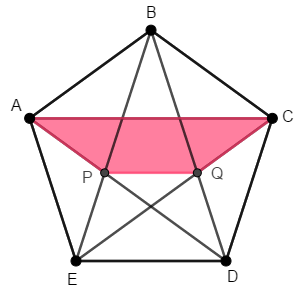
Calcule a área do quadrilátero [tex]APQC[/tex].

Ajuda
(1) A medida em graus de cada ângulo interno de um pentágono regular é [tex] 108^\circ \, .[/tex] (Se precisar, visite esta Sala.)
(2) A soma dos ângulos internos de qualquer triângulo é [tex]180^\circ[/tex].
(3) Se dois lados de um triângulo são proporcionais a dois lados de outro triângulo e os ângulos internos definidos por esses lados são congruentes, então os triângulos são semelhantes pelo caso L.A.L..
(Há uma Sala de Ajuda sobre semelhança de triângulos no nosso Blog!)
(4) Se dois ângulos de um triângulo são congruentes a dois ângulos de outro triângulo e os lados definidos entre esses dois ângulos são congruentes, então os triângulos são congruentes pelo caso A.L.A..
(Se você não se lembra dos casos de congruência entre triângulos, clique AQUI.)
Notações:
– Denotaremos o segmento definido por dois pontos, digamos [tex]X[/tex] e [tex]Y[/tex], por [tex]\overline {XY} [/tex] e o seu comprimento por [tex]XY.[/tex]
– Denotaremos a medida de um ângulo [tex]X \hat YZ[/tex] por [tex]\lt X \hat YZ\gt.[/tex]
Problema
(Indicado a partir do 9º ano do E. F.)
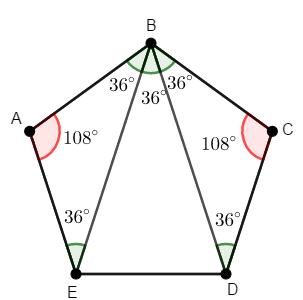
Inicialmente, notemos que as diagonais do pentágono regular dividem cada ângulo interno em três ângulos congruentes. Para ilustrar esse fato, considere por exemplo o ângulo [tex]B[/tex] do nosso pentágono regular.
- Com efeito, como os triângulos [tex]EAB[/tex] e [tex]BCD[/tex] são isósceles (uma vez que o pentágono é regular), os ângulos da base, "[tex]B \hat E A[/tex] e [tex]E \hat B A[/tex]", assim como "[tex]B \hat D C[/tex] e [tex]D \hat B C [/tex]", têm a mesma medida. Pelo Lembrete (1) a medida dos ângulos "[tex]E \hat A B[/tex] e [tex]B \hat C D[/tex]" é [tex] 108^\circ \, [/tex]; portanto, utilizando o Lembrete (2), a medida [tex]\alpha[/tex], em graus, de cada um dos ângulos [tex]B \hat E A[/tex], [tex]E \hat B A[/tex], [tex]B \hat D C[/tex] e [tex]C \hat D B[/tex] pode ser assim calculada:
[tex]\qquad \alpha=\dfrac{180^\circ-108^\circ}{2}=36^\circ \, .\\ \,[/tex]
Como o ângulo [tex]A \hat B C[/tex] mede também [tex] 108^\circ \, [/tex] e os ângulos [tex]A \hat B E[/tex] e [tex]D \hat B C[/tex] medem [tex] 36^\circ \, [/tex] cada, a medida do ângulo [tex]E \hat B D[/tex] é dada por:
[tex]\qquad 108^\circ-36^\circ \,-36^\circ \,=36^\circ .[/tex]
Para encontrar a área do quadrilátero [tex]APQC[/tex], vamos considerar [tex]R[/tex] o ponto de interseção dos segmentos [tex]\overline{AC}[/tex] e [tex]\overline{BD}[/tex], [tex]T[/tex] o ponto de interseção dos segmentos [tex]\overline{AC}[/tex] e [tex]\overline{BE}[/tex], [tex]U[/tex] o ponto de interseção dos segmentos [tex]\overline{AD}[/tex] e [tex]\overline{CE}[/tex] e o segmento [tex]\overline{PR}[/tex].
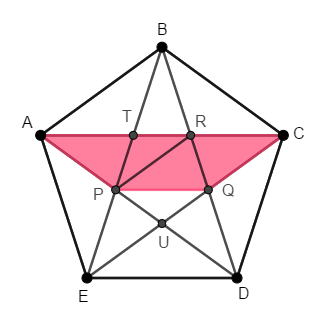
Considerando todas as diagonais do pentágono [tex]ABCDE[/tex], concluímos que os triângulos [tex]TAB[/tex], [tex]RBC[/tex], [tex]QCD[/tex], [tex]UDE[/tex] e [tex]PEA[/tex] são isósceles e congruentes. Dessa forma, [tex]AT=TB=BR=RC=CQ=QD=UD=UE=PE=PA[/tex] e, então os triângulos [tex]ATP[/tex], [tex]BRT[/tex], [tex]CQR[/tex], [tex]DUQ[/tex] e [tex]EPU[/tex] são isósceles e congruentes, de acordo com o Lembrete (3). Consequentemente, esses triângulos possuem a mesma área, a qual denotaremos por [tex]S_1[/tex].
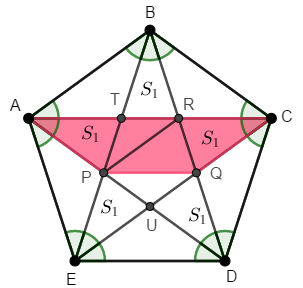
Observamos que o triângulo [tex]PRQ[/tex] também tem área [tex]S_1[/tex]. Para justificar essa afirmação, vamos mostrar que o triângulo [tex]RPQ[/tex] é congruente ao triângulo [tex]RCQ[/tex].
- No triângulo isósceles [tex]ATP[/tex] temos que [tex]\lt T\hat{A}P\gt=36^{\circ}[/tex], [tex]\lt A\hat{P}T\gt=\lt A\hat{T}P\gt=72^{\circ}[/tex].
- No triângulo isósceles [tex]CRQ[/tex] temos que [tex]\lt R\hat{C}Q\gt=36^{\circ}[/tex], [tex]\lt C\hat{R}Q\gt=\lt C\hat{Q}R\gt=72^{\circ}[/tex].
- Sendo o ângulo [tex]R\hat{T}P[/tex] oposto pelo vértice ao ângulo [tex]B\hat{T}A[/tex], então [tex]\lt B\hat{T}A\gt=\lt R\hat{T}P\gt=108^{\circ}[/tex]. Como [tex]TP=TR[/tex], temos que o triângulo [tex]PTR[/tex] é isósceles; logo, [tex]\lt T\hat{P}R\gt=\lt T\hat{R}P\gt=36^{\circ}[/tex].
- Como [tex]\lt A\hat{R}C\gt=180^{\circ}[/tex], [tex]\lt T\hat{R}P\gt=36^{\circ}[/tex] e [tex]\lt C\hat{R}Q\gt=72^{\circ}[/tex] então [tex]\lt P\hat{R}Q\gt=72^{\circ}[/tex].
- Sendo o ângulo [tex]P\hat{U}Q[/tex] oposto pelo vértice ao ângulo [tex]E\hat{U}D[/tex], então [tex]\lt P\hat{U}Q\gt=\lt E\hat{U}D\gt=108^{\circ}[/tex]. Como [tex]PU=QU[/tex], temos que o triângulo [tex]PUQ[/tex] é isósceles; logo, [tex]\lt U\hat{P}Q\gt=\lt U\hat{Q}P\gt=36^{\circ}[/tex].
- Como [tex]\lt C\hat{Q}E\gt=180^{\circ}[/tex], [tex]\lt C\hat{Q}R\gt=72^{\circ}[/tex] e [tex]\lt U\hat{Q}P\gt=36^{\circ}[/tex] então [tex]\lt P\hat{Q}R\gt=72^{\circ}[/tex].
Assim, o triângulo [tex]RPQ[/tex] é isósceles de base [tex]\overline{RQ}[/tex] e [tex]\lt R\hat{P}Q\gt=36^{\circ}[/tex]. Pelo Lembrete (4), temos que os triângulos [tex]RPQ[/tex] e [tex]RCQ[/tex] são congruentes. Logo, o triângulo [tex]PRQ[/tex] tem área [tex]S_1[/tex].
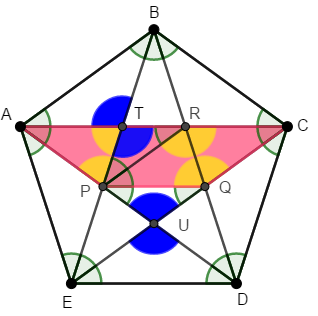
Como o triângulo [tex]RPQ[/tex] é isósceles de base [tex]\overline{RQ}[/tex], temos que [tex]PR=PQ[/tex]. Na figura acima, os triângulos [tex]TPR[/tex] e [tex]UPQ[/tex] são congruentes, pelo Lembrete (4), e possuem mesma área, que denotaremos por [tex]S_2[/tex].
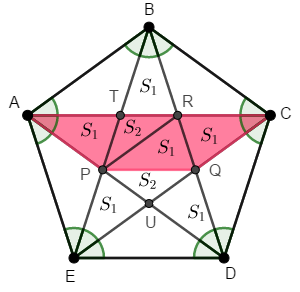
Finalmente, já podemos calcular a área do quadrilátero [tex]APQC[/tex], que denotaremos por [tex]A_{APQC}[/tex]. Para isso, observe que:
– a área do quadrilátero [tex]APQC[/tex] é [tex]\boxed{3S_1+S_2}[/tex] e
– a área da estrela [tex]EBDAC[/tex] é [tex]\boxed{6S1+2S_2}[/tex];
assim, como [tex]\boxed{6S1+2S_2=1}[/tex], temos que:
[tex]\qquad A_{APQC}=3S_1+S_2[/tex]
[tex]\qquad A_{APQC}=\dfrac{6S_1+2S_2}{2}[/tex]
[tex]\qquad A_{APQC}=\dfrac{1}{2}.[/tex]
Portanto, a área do quadrilátero [tex]APQC[/tex] é [tex]\, \fcolorbox{black}{#eee0e5}{$\dfrac{1}{2}$}\, [/tex] unidade de área.
Solução elaborada pelos Moderadores do Blog.
