Problema
(Indicado a partir do 8º ano do E. F.)
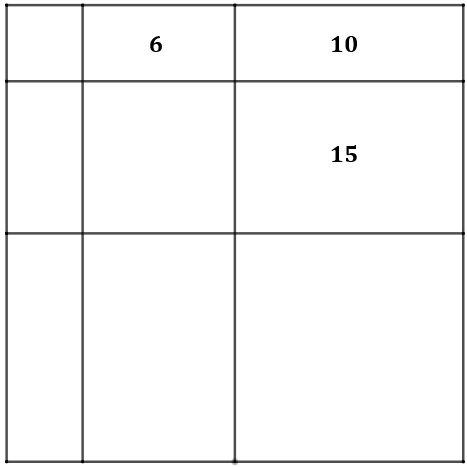
Na figura abaixo temos um quadrado que foi repartido em [tex]9[/tex] regiões menores ([tex]3[/tex] quadrados e [tex]6[/tex] retângulos). As áreas de três retângulos estão indicadas na figura.
Qual a área total da figura?
Solução
Vamos denotar por [tex]\textcolor{#0000FF}{a}[/tex], [tex]\textcolor{#FF0000}{b}[/tex] e [tex]\textcolor{#400080}{c}[/tex] as medidas dos lados dos [tex]3[/tex] quadrados internos. Observe a próxima figura.
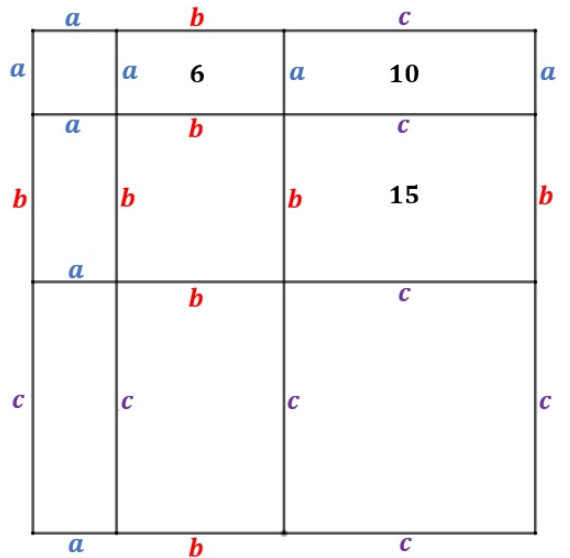
A partir das três áreas conhecidas, não é difícil concluir que:
[tex]\qquad a\cdot b=6[/tex]; [tex]\textcolor{#800000}{(i)}[/tex]
[tex]\qquad a\cdot c=10[/tex]; [tex]\textcolor{#800000}{(ii)}[/tex]
[tex]\qquad b\cdot c=15[/tex].[tex]\textcolor{#800000}{(iii)}[/tex]
De [tex]\textcolor{#800000}{(i)}\,[/tex] e [tex]\, \textcolor{#800000}{(ii)}[/tex], segue que:
[tex]\qquad \dfrac{b}{c}=\dfrac{6}{10}=\dfrac{3}{5}[/tex];
assim,
[tex]\qquad b=\dfrac{3}{5}c\qquad \textcolor{#800000}{(iv)}[/tex].
Substituindo [tex]\textcolor{#800000}{(iv)}\, [/tex] em [tex]\, \textcolor{#800000}{(iii)}[/tex], obtemos [tex]\dfrac{3}{5}c^2=15[/tex], donde [tex]c^2=25[/tex]. Como [tex]c[/tex] é uma medida, seu valor é positivo; assim, podemos concluir que [tex]\boxed{c=5}[/tex], [tex]\boxed{b=3}[/tex] e [tex]\boxed{a=2}[/tex].
Com isso, obtemos as áreas dos demais quadriláteros da figura inicial, conforme indicamos a seguir.
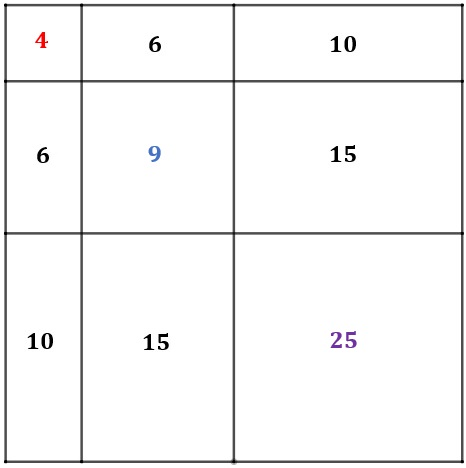
Portanto, a área total da figura é [tex]6+10+15+6+10+15+4+9+25=100[/tex] unidades de área.
Este problema é uma ilustração da interpretação geométrica de um dos mais famosos produtos notáveis – O Quadrado da soma de três termos:
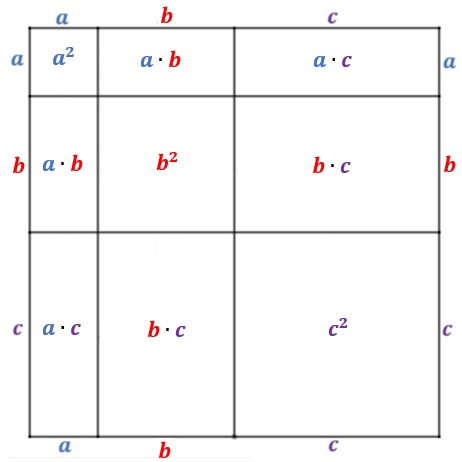
Solução elaborada pelos Moderadores do Blog.
