Problema
(Indicado a partir do 9º ano do E. F.)
Dados um triângulo qualquer [tex]RST[/tex] e um número real positivo [tex]h[/tex], você é capaz de construir outro triângulo que tenha a mesma área do triângulo [tex]RST[/tex] e uma de suas alturas com comprimento [tex]h[/tex]?
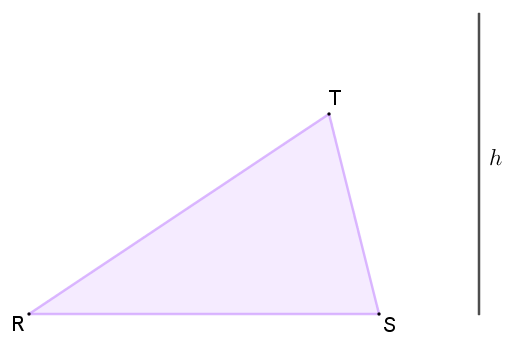
Descreva a sua construção.
(Você não precisa saber fazer as construções, necessariamente, já que algumas delas talvez precisem ser feitas com régua e compasso.)

AJUDA
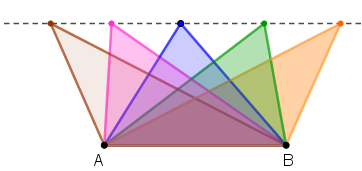
Todos os triângulos que são obtidos movendo-se um vértice de um dado triângulo paralelamente ao lado oposto a esse vértice têm a mesma área.
Solução
Uma construção que atende as condições do problema é a que descrevemos a seguir.
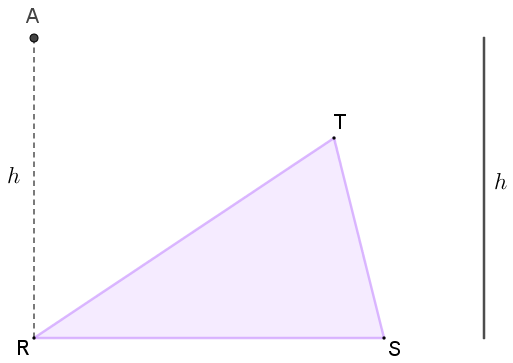
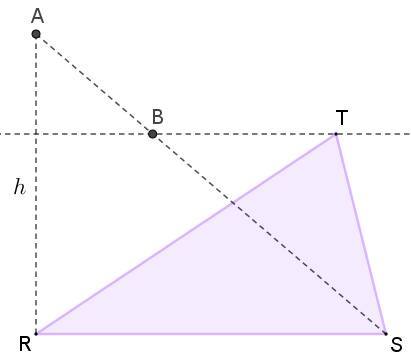
- Traçar o segmento de reta [tex]AR[/tex] perpendicular ao segmento [tex]RS[/tex] e com comprimento [tex]h.[/tex]
- Traçar o segmento [tex]AS[/tex].
- Traçar uma reta paralela ao segmento [tex]RS[/tex] por [tex]T[/tex]. Essa reta corta o segmento [tex]AS[/tex] em [tex]B.[/tex]
- De acordo com a AJUDA, os triângulos [tex]RST\,[/tex] e [tex]\,RSB\,[/tex] têm a mesma área.[tex]\qquad \qquad \textcolor{#800000}{(i)} [/tex]
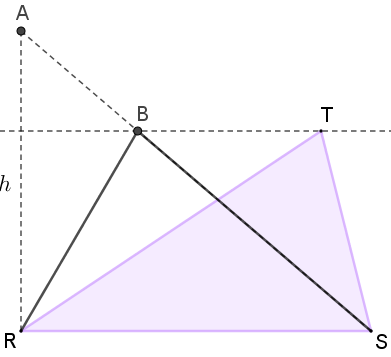
- Traçar por [tex]B[/tex] uma reta paralela ao segmento [tex]AR[/tex]. Essa reta corta o segmento [tex]RS[/tex] em [tex]C.[/tex]
- De acordo com a AJUDA, os triângulos [tex]BCA\,[/tex] e [tex]\,BCR\,[/tex] têm a mesma área.[tex]\qquad \qquad \textcolor{#800000}{(ii)} [/tex]
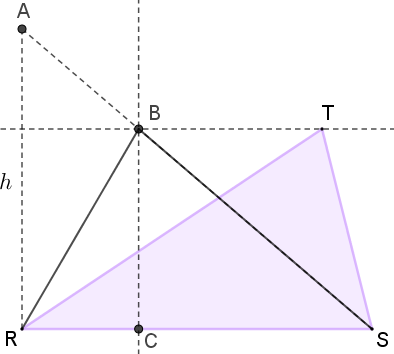
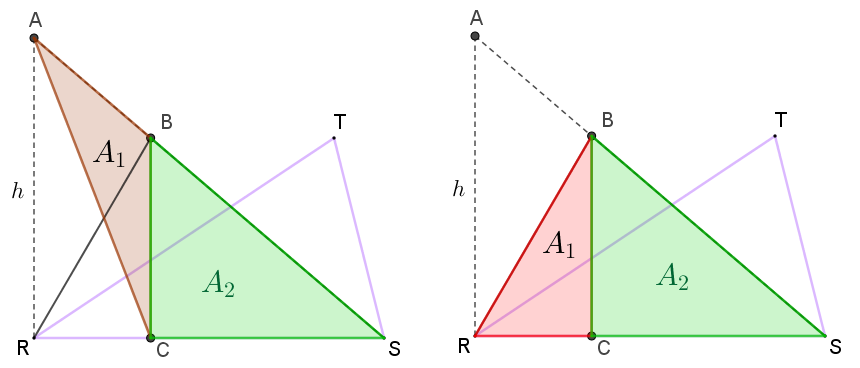
- Observe, agora, que a área do triângulo [tex]ACS\,[/tex] pode ser escrita como a soma das áreas dos triângulos [tex]ACB\,[/tex] e [tex]\,BCS\,[/tex], conforme mostra a figura abaixo, à esquerda. Por outro lado, a área do triângulo [tex]RSB\,[/tex] pode ser escrita como a soma das áreas dos triângulos [tex]RCB\,[/tex] e [tex]\,BCS\,[/tex], de acordo com a figura abaixo, à direita.
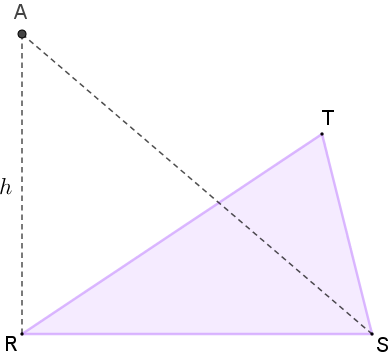
De fato, se tomarmos o segmento [tex]RS[/tex] como base de ambos, eles terão alturas com o mesmo comprimento.
De fato, se tomarmos o segmento [tex]BC[/tex] como base de ambos, eles terão alturas com o mesmo comprimento. Vamos supor que a medida dessa área seja [tex]A_1.[/tex]
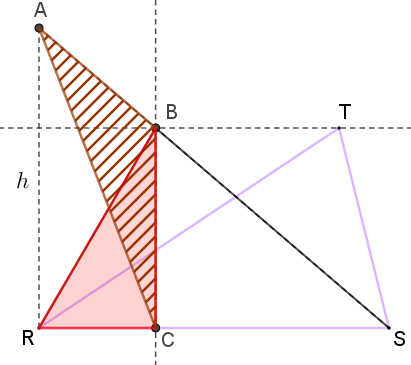
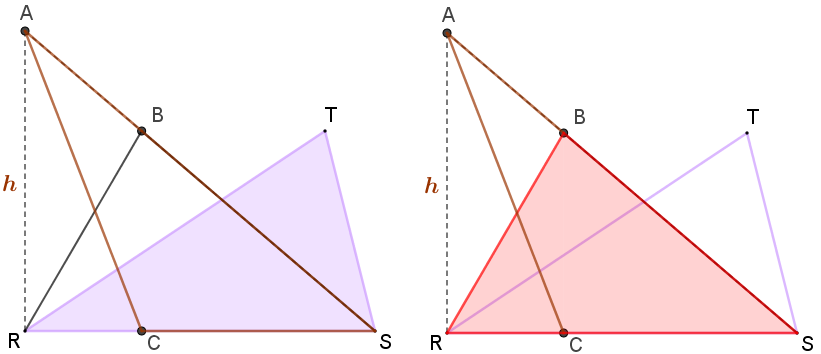
Assim, por [tex] \textcolor{#800000}{(ii)} [/tex], os triângulos [tex]RBS\,[/tex] e [tex]ACS\,[/tex] têm a mesma área. [tex]\qquad \qquad \textcolor{#800000}{(iii)} [/tex]
Finalmente, observe que:
- Por [tex]\textcolor{#800000}{(i)} [/tex], os triângulos [tex]RST\,[/tex] e [tex]\,RSB\,[/tex] têm a mesma área.
- Por [tex]\textcolor{#800000}{(iii)} [/tex], os triângulos [tex]RBS\,[/tex] e [tex]ACS\,[/tex] têm a mesma área.
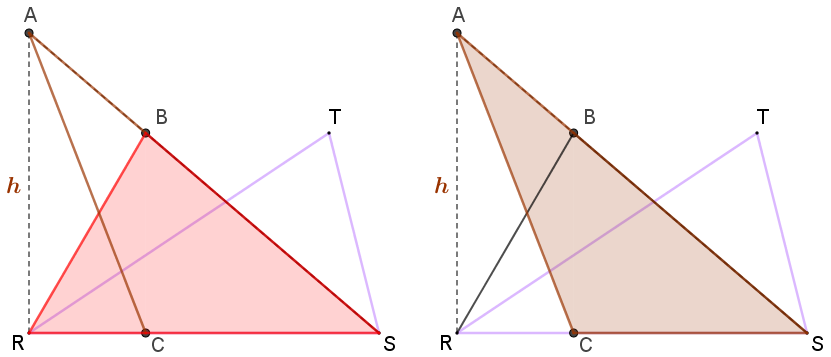
Dessa forma, o triângulo [tex]ACS\,[/tex] tem a mesma área do triângulo [tex]RST[/tex] e uma de suas alturas tem comprimento [tex]h.[/tex]
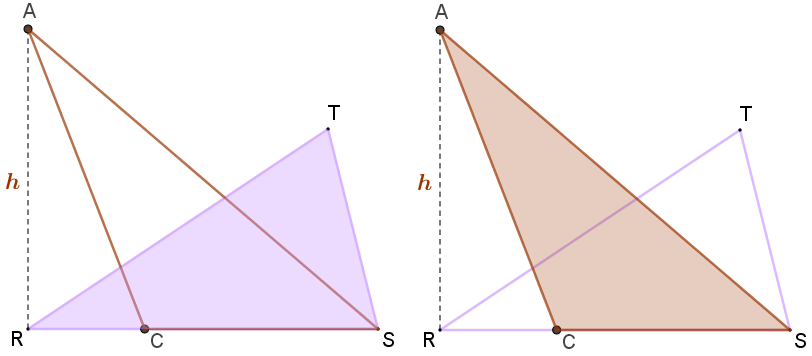
Solução elaborada pelos Moderadores do Blog.
