Problema
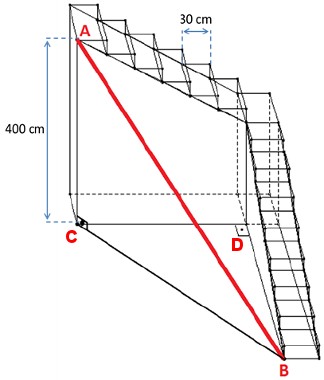
(IFSC – Adaptado) Para acessar o topo de uma plataforma de saltos a [tex]400[/tex] cm de altura, um atleta deve subir uma escadaria que possui [tex]8[/tex] degraus no primeiro lance e [tex]6[/tex] degraus no segundo lance de escada, conforme mostra a figura.
Sabendo que cada degrau possui [tex]30[/tex] cm de profundidade, qual o comprimento, em cm, da haste metálica [tex]\overline{AB}[/tex] utilizada para dar sustentação à plataforma?

Lembrete
Teorema de Pitágoras: Em um triângulo retângulo, o quadrado da hipotenusa é a soma dos quadrados dos catetos.
Solução
Observe a figura do problema e perceba que, para calcular o comprimento da barra [tex]\overline{AB}[/tex], é necessário descobrir primeiro o comprimento da barra [tex]\overline{BC}[/tex]. Apliquemos, então, o Teorema de Pitágoras no triângulo [tex]BCD[/tex].
Como os catetos [tex]\overline{BD}[/tex] e [tex]\overline{CD}[/tex] medem, respectivamente, [tex]\boxed{8\cdot 30=240 \,cm}[/tex] e [tex]\boxed{6\cdot 30=180\,cm}[/tex], segue que:
[tex]\qquad (BC)^2=240^2+180^2[/tex]
[tex]\qquad BC=300\, cm.[/tex]
Considerando o triângulo [tex]ABC[/tex], cujos catetos, agora conhecidos, medem [tex]400[/tex] cm e [tex]300[/tex] cm, poderemos utilizar o Teorema de Pitágoras para calcular o comprimento da haste [tex]\overline{AB}.[/tex] Assim:
[tex]\qquad(AB)^2=400^2+300^2[/tex]
[tex]\qquad AB=500[/tex],
ou seja, o comprimento da haste metálica [tex]\overline{AB}[/tex] é [tex]\, \fcolorbox{black}{#eee0e5}{$500\, cm$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
