Problema
(Indicado a partir do 2º ano do E. M.)
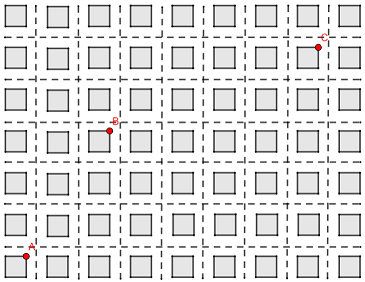
Na figura abaixo, temos a planta de uma região de um bairro, sendo que os pontos assinalados com as letras [tex]\textcolor{red}{A}[/tex], [tex]\textcolor{red}{B}[/tex] e [tex]\textcolor{red}{C} [/tex] são, respectivamente, a academia, o supermercado e a casa de João. Ele quer percorrer o caminho do ponto [tex]\textcolor{red}{A}[/tex] ao ponto [tex]\textcolor{red}{C}[/tex] passando por [tex]\textcolor{red}{B}[/tex] com as seguintes restrições: ele pode ir da esquerda para a direita e de baixo para cima. Quantos caminhos diferentes João poderia percorrer de [tex]\textcolor{red}{A}[/tex] até [tex]\textcolor{red}{C}[/tex]?
Lembretes:

✏ Uma das maneiras de agruparmos elementos de um dado conjunto é escolhê-los levando-se em consideração apenas a sua natureza, sem se importar em que ordem eles foram escolhidos ou apresentados. Esse tipo de agrupamento de elementos é denominado uma Combinação simples. Especificamente, quando escolhemos [tex]r[/tex] dentre [tex]n[/tex] elementos de um conjunto dessa forma, dizemos que estamos definindo uma Combinação simples de [tex]n[/tex] elementos tomados [tex]r[/tex] a [tex]r[/tex].
E o legal é que, dado um conjunto finito, podemos determinar quantos agrupamentos desse tipo podemos fazer, sem que precisemos exibi-los.
- O número de Combinações simples de [tex]n[/tex] elementos, tomados [tex]r[/tex] a [tex]r[/tex], é denotado por [tex]C_{n\, ,\, r}[/tex] ou [tex]C_n^r[/tex] e assim definido:
[tex]C_{n\, ,\, r}=C_n^r=\dfrac{n!}{(n-r)!\, r!} \text{, com } n,r \in\mathbb{N} \text{ e }\, r\leqslant n[/tex].
O quociente [tex]\dfrac{n!}{(n-r)!\, r!}[/tex] também pode ser denotado por [tex]\dbinom{n}{r}[/tex] e nesse caso é denominado coeficiente binomial ou número binomial.
✏ Princípio Fundamental da Contagem, ou Princípio Multiplicativo, para duas decisões:
Se uma decisão D1 pode ser tomada de [tex] m [/tex] maneiras distintas e, tomada essa decisão D1, uma decisão D2 puder ser tomada de [tex] n [/tex] maneiras distintas, então a quantidade de maneiras de se tomar sucessivamente as decisões D1 e D2 é igual a [tex]~\boxed{ m \times n}\, . [/tex]
Solução
Vamos analisar isoladamente as quadras a serem percorridas de [tex]\textcolor{red}{A}[/tex] até [tex]\textcolor{red}{B}[/tex] e de [tex]\textcolor{red}{B}[/tex] até [tex]\textcolor{red}{C}.[/tex]
- Qualquer que seja o percurso escolhido de [tex]\textcolor{red}{A}[/tex] até [tex]\textcolor{red}{B}[/tex], João deverá caminhar [tex]2[/tex] quadras da esquerda para a direita e [tex]3[/tex] quadras para cima. Além disso, em cada esquina, João deve escolher: vou “para cima” ou “para a direita”?
Para ir de [tex]\textcolor{red}{A}[/tex] até [tex]\textcolor{red}{B}[/tex], com as restrições impostas, temos um total de [tex]2+ 3=5[/tex] quadras a serem percorridas. Em exatamente [tex] 3 [/tex] delas, João irá para cima, sendo que a decisão de ir para cima pode ser tomada de qualquer esquina saindo de [tex]\textcolor{red}{A}[/tex] até chegar em [tex]\textcolor{red}{B}.[/tex] Perceba que, escolhidas as [tex]3[/tex] quadras nas quais João irá para cima, as outras [tex]2[/tex] ficam previamente determinadas; assim, do conjunto de percursos que envolvem [tex]5[/tex] quadras, João pode selecionar [tex]3[/tex] desses para serem percursos para cima. Logo, há - De maneira análoga, chegando em [tex]\textcolor{red}{B}[/tex], João deverá caminhar [tex]5[/tex] quadras da direita para a esquerda e [tex]2[/tex] quadras para cima para chegar no ponto [tex]\textcolor{red}{C}.[/tex] Aqui também, escolhendo-se duas quadras, as outras cinco ficam previamente determinadas. Portanto, há
[tex] \qquad \qquad {\left( \begin{array}{c} 5 \\ 3 \end{array} \right)} = \dfrac{5!}{ 3!\cdot 2!} = \dfrac{ 5 \cdot 4 \cdot 3!}{ 3!\cdot 2!} = \dfrac{ 5 \cdot 4}{ 2} =10 [/tex] percursos distintos saindo de [tex]\textcolor{red}{A}[/tex] e chegando em [tex]\textcolor{red}{B}[/tex].
[tex] \qquad \qquad {\left( \begin{array}{c} 7 \\ 2 \end{array} \right)} = \dfrac{7!}{ 5!\cdot 2!} = \dfrac{ 7 \cdot 6 \cdot 5!}{ 5!\cdot 2!} = \dfrac{ 7 \cdot 6}{ 2} =21 [/tex] percursos distintos saindo de [tex]\textcolor{red}{B}[/tex] e chegando em [tex]\textcolor{red}{C}.[/tex]
Finalmente, segue do Princípio Multiplicativo que João pode fazer [tex]\fcolorbox{black}{#eee0e5}{$10 \cdot 21=210$} [/tex] percursos diferentes saindo de [tex]\textcolor{red}{A}[/tex] e indo até [tex]\textcolor{red}{C}[/tex], passando por [tex]\textcolor{red}{B}[/tex].
Solução elaborada pelos Moderadores do Blog.
