Problema
(Indicado a partir do 9º ano do E. F.)
(Simulado do colégio Ari de Sá – Fortaleza) A seguir, vemos parte do mapa de uma cidade cujas vias são de mão única. Neste mapa, está indicada a quantidade média de veículos que trafegam em cada rua por minuto.
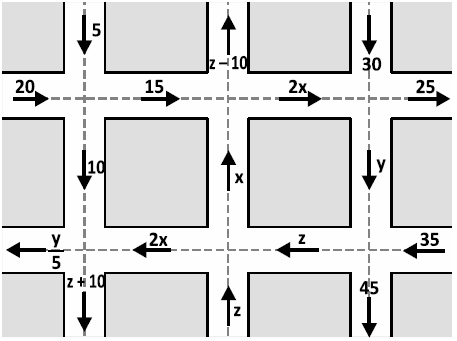
Sendo [tex]x+y–z[/tex] o número de veículos que atravessam certo cruzamento por minuto, determine o número médio de veículos que atravessam esse cruzamento em uma hora.
Solução
Observe os seguintes cruzamentos:
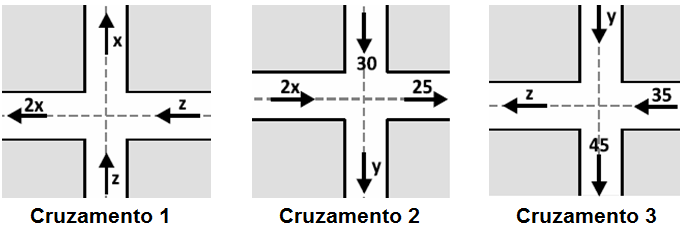
A partir desses cruzamentos, podemos escrever as seguintes equações:
- Cruzamento 1: [tex]2z=3x[/tex];
- Cruzamento 2: [tex]2x+30=25+y[/tex];
- Cruzamento 3: [tex]y+35=z+45[/tex].
Da equação do Cruzamento 1 temos que [tex]\boxed{z=\dfrac{3x}{2}}[/tex] e da equação do Cruzamento 2 podemos tirar que [tex]\boxed{y=2x+5}[/tex].
Agora, substituindo essas duas últimas expressões na equação do Cruzamento 3, segue que:
[tex]\qquad y+35=z+45 \\
\qquad 2x+5+35=\dfrac{3x}{2}+45 \\
\qquad x=10[/tex]
e, portanto, [tex]z=\dfrac{3 \cdot 10}{2}=15[/tex] e [tex]y=2 \cdot 10+5=25[/tex].
Finalmente, como [tex]x+y–z=10+25-15=20[/tex] é o número de veículos que atravessam certo cruzamento por minuto, então o número médio de veículos que atravessam esse cruzamento em uma hora é [tex]~\fcolorbox{black}{#eee0e5}{$20 \cdot 60=1200$}~.[/tex]
Solução elaborada pelos Moderadores do Blog.
