✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Médio)
Duas famílias, os Silva e os Oliveira, marcaram um jantar de confraternização em um restaurante. No dia do encontro, compareceram 20 pessoas para o jantar.
Cada membro da família Silva gastou R$ 40,00, os Oliveira gastaram R$ 50,00 cada e o total das despesas foi de R$ 880,00.
Quantos membros de cada família participaram do jantar?
Represente geometricamente a sua solução.
Solução
Vamos denotar por [tex]o\, [/tex] e [tex]\, s[/tex], respectivamente, a quantidade de membros das famílias Oliveira e Silva que participaram do jantar. Assim, podemos escrever matematicamente as informações dadas no problema e obter o seguinte sistema de equações do 1º grau:
[tex]\qquad \qquad S_1: \begin{cases}
o+s=20\\
40s+50o=880\end{cases}[/tex] ,
que pode ser simplificado, se dividirmos a segunda equação por [tex]10[/tex]:
[tex]\qquad \qquad S_2:\begin{cases}
o+s=20\\
4s+5o=88\end{cases}[/tex] .
[tex]\textcolor{#800000}{(i)}[/tex] Para determinar quantos membros de cada família participaram do jantar, vamos resolver o sistema [tex]S_2[/tex]. Para isso, vamos inicialmente multiplicar a primeira equação por [tex]-4[/tex] e somar a equação resultante com a segunda equação:
[tex]\qquad \qquad \begin{array}{c l}
-4s-4o=-80 & +\\
4s+5o=88&\\
0s+ o=8&
\hline
\end{array}[/tex].
Assim, obtemos que [tex]\boxed{o=8}\,\,\,\,\,\,.[/tex]
Substituindo o valor encontrado na primeira equação de [tex]S_2[/tex], segue que:
[tex]\qquad \qquad o+s=20\\
\qquad \qquad 8+s=20\\
\qquad \qquad s=20-8\\
\qquad \qquad \boxed{s=12}.[/tex]
Podemos então concluir que participaram do jantar oito membros da família Oliveira e doze membros da família Silva.
[tex]\textcolor{#800000}{(ii)}[/tex] Podemos representar graficamente a solução algébrica que obtivemos observando que, fixado um plano cartesiano [tex]sOo[/tex], as equações [tex]\boxed{o+s=20}[/tex] e [tex]\boxed{4s+5o=88}[/tex] representam duas retas transversais:
- fazendo [tex]o=0[/tex] e [tex]s=0[/tex] em [tex]\boxed{o+s=20}[/tex], obtemos os pontos nos quais a reta definida por essa equação intersecta os eixos [tex]Os[/tex] e [tex]Oo[/tex], respectivamente: [tex](20,0)[/tex] e [tex](0,20)[/tex];
- fazendo [tex]o=0[/tex] e [tex]s=0[/tex] em [tex]\boxed{4s+5o=88}[/tex], obtemos os pontos nos quais a reta definida por essa equação intersecta os eixos [tex]Os[/tex] e [tex]Oo[/tex], respectivamente: [tex](22,0)[/tex] e [tex](\frac{88}{5},0)[/tex] (observe que [tex]\frac{88}{5}=17,6).[/tex]
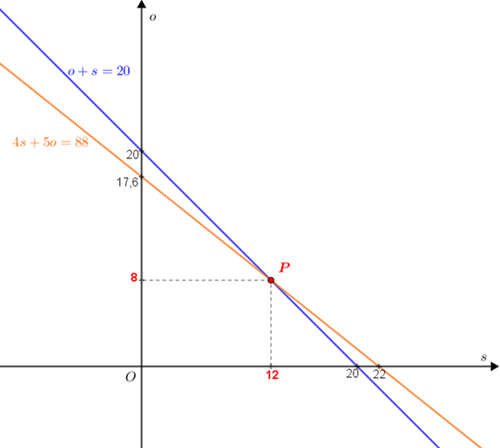
Para efeito do nosso problema, nem todos os pontos das retas nos interessam, já que estamos interessados em valores de [tex]o[/tex] e de [tex]s[/tex] que representem quantidades de pessoas. Portanto, dos pontos das duas retas, apenas aqueles que têm as duas coordenadas naturais traduziriam possíveis soluções do problema.
Em particular, as coordenadas do ponto de interseção das duas retas, [tex]P=\left(12,8\right)[/tex], fornece a solução do problema: [tex]\fcolorbox{black}{#eee0e5}{$o=8$}[/tex] e [tex]\fcolorbox{black}{#eee0e5}{$s=12$}.[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
