Problema
(Indicado a partir do 9º ano do E. F.)
(Simulado do Colégio Ari de Sá, Fortaleza) Na figura abaixo, temos três circunferências tangentes entre si duas a duas.
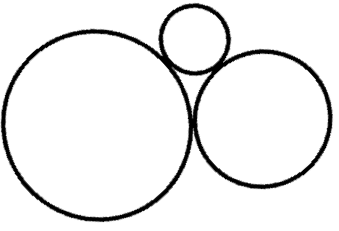
O triângulo com vértices nos centros das circunferências tem lados que medem [tex]6\, cm[/tex] , [tex]7\, cm [/tex] e [tex]9\, cm.[/tex] Qual é a soma dos perímetros (comprimentos) das circunferências?
Solução
Observe a figura a seguir, na qual [tex]a, b, c[/tex] são as medidas, em centímetros, dos raios das três circunferências.
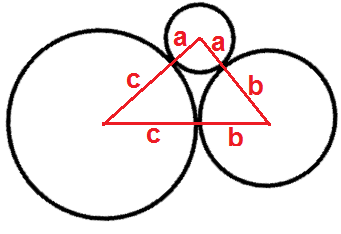
Podemos, então, escrever que:
[tex]
\qquad \begin{cases}
a+b=6\\
a+c=7\\
b+c=9
\end{cases}\\
\qquad \qquad [/tex] .
Adicionando as três equações, obtemos: [tex]2a+2b+2c=22[/tex], e, dividindo esta última equação por [tex]2[/tex], obtemos [tex]\boxed{a+b+c=11}.[/tex]
Por outro lado, a soma dos perímetros das circunferências é dada por:
[tex]\qquad 2\cdot \pi \cdot a+2\cdot \pi \cdot b+2\cdot \pi \cdot c=2\cdot \pi \cdot (a+b+c)= 2\cdot \pi \cdot 11=\fcolorbox{black}{#eee0e5}{$22\pi \ cm$}\, [/tex],
aproximadamente, [tex]\fcolorbox{black}{#eee0e5}{$69\ cm$}\, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
