Problema
(Indicado a partir do 8º ano do E. F.)
(Simulado do Colégio Ari de Sá, Fortaleza) O mosaico mostrado na figura foi construído com peças retangulares brancas, todas iguais, e peças quadradas cinzas, todas iguais.
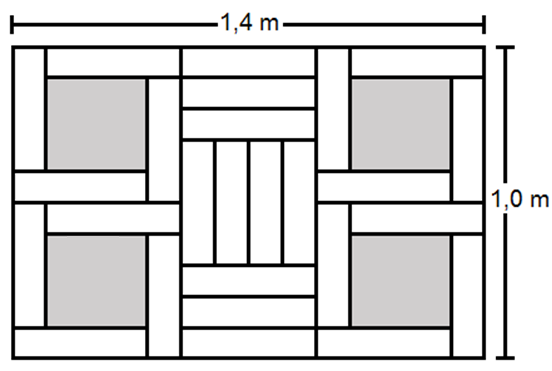
Qual o valor da área cinza?
Solução
Considere [tex]x[/tex] e [tex]y[/tex] as medidas em metros das dimensões de cada peça retangular. Conhecidas essas duas medidas, observe que os lados das peças quadradas ficam automaticamente definidos.
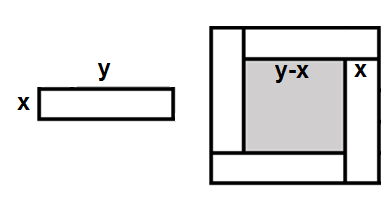
A partir das informações contidas na figura do enunciado, temos que [tex]2x+2y=1[/tex] e [tex]2x+3y=1,4[/tex]. Subtraindo essas duas igualdades, segue que:
[tex]\qquad 2x+3y-(2x+2y)=1,4-1[/tex]
[tex]\qquad 2x+3y-2x-2y=0,4[/tex]
[tex]\qquad \boxed{y=0,4}.[/tex]
Substituindo esse valor na equação [tex]2x+2y=1[/tex], vem que:
[tex]\qquad 2x+2\cdot 0,4=1[/tex]
[tex]\qquad 2x+0,8=1[/tex]
[tex]\qquad 2x=0,2[/tex]
[tex]\qquad \boxed{x=0,1}.[/tex]
Com isso, temos que:
- o lado do quadrado cinza é [tex]\boxed{y-x=0,4-0,1=0,3\, m}[/tex],
- a medida da área de cada quadrado cinza é [tex]\boxed{ \left(y-x\right)^2=0,3^2=0,09 \ m^2}.[/tex]
Portanto, o valor da área cinza total do mosaico é [tex]\, \fcolorbox{black}{#eee0e5}{$4\times 0,09=0,36 \ m^2$}\, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
