Problema
(Indicado a partir do 9º ano do E. F.)
Seu João é dono de uma imobiliária e comprou os terrenos [tex]\textbf{A, B}[/tex] e [tex]\textbf{C}[/tex], indicados na figura abaixo.
As divisas laterais que aparecem na figura são perpendiculares à Rua das Flores, as frentes dos terrenos ficam na Rua dos Pássaros e as medidas das três frentes somam [tex]180\;m[/tex].
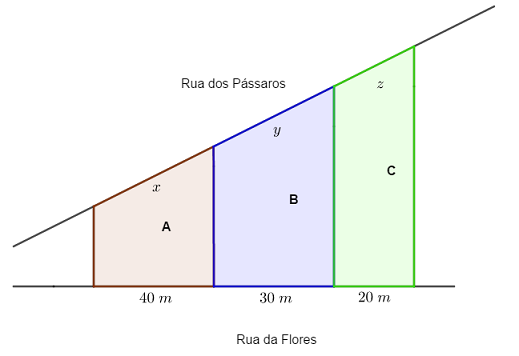
Como o seu João ainda não construiu casas nos terrenos, pelas leis municipais, ele deverá construir uma mureta na frente de cada um dos terrenos. A mureta do terreno [tex]A[/tex] será construída com [tex]50\;cm[/tex] de altura, a do terreno [tex]B[/tex] com [tex]40\;cm[/tex] de altura e a do terreno [tex]C[/tex] com [tex]60\;cm[/tex], todas com a mesma espessura.
Sabendo que o metro quadrado de mureta construída com a espessura em questão custa [tex]R\$\;10,00[/tex], quanto seu João gastará?

Lembretes
(1) Teorema de Tales: Se duas retas são transversais de um feixe de retas paralelas, então a razão entre dois segmentos quaisquer de uma delas é igual à razão entre os respectivos segmentos correspondentes da outra.
Regras de Proporcionalidade:
(2) Se [tex]\dfrac{a}{b}=\dfrac{c}{d}[/tex], então [tex]a\cdot d=b\cdot c\\
[/tex].
(3) Se[tex]\dfrac{a}{b}=\dfrac{c}{d}[/tex], então [tex]\dfrac{a}{b}=\dfrac{c}{d}=\dfrac{a+c}{b+d}.[/tex]
Solução
- Primeiro, precisamos determinar as medidas das frentes dos terrenos, ou seja, [tex]x, y[/tex] e [tex]z[/tex].
- Agora, vamos calcular as medidas das áreas das três muretas.
Usando o Teorema de Tales, Lembrete (1), temos que
[tex]\\
\qquad \qquad \dfrac{x}{40}=\dfrac{y}{30}=\dfrac{z}{20}.\\
[/tex]
Assim, pelo Lembrete (3) concluímos que:
[tex]\\
\qquad \qquad \dfrac{x}{40}=\dfrac{y}{30}=\dfrac{z}{20}=\dfrac{x+y+z}{40+30+20}.\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \textcolor{#800000}{(i)}\\
[/tex]
Sabemos que [tex]x+y+z=180[/tex], substituindo em [tex]\textcolor{#800000}{(i)}[/tex] temos:
[tex]\\
\qquad \qquad \dfrac{x}{40}=\dfrac{y}{30}=\dfrac{z}{20}=\dfrac{180}{90}.\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\textcolor{#800000}{(ii)}\\
[/tex]
Logo, usando o Lembrete (2) nas igualdades [tex]\textcolor{#800000}{(ii)}[/tex], segue que:
[tex] \qquad \qquad \dfrac{x}{40}=\dfrac{180}{90} \Rightarrow 90\cdot x= 40 \cdot 180\Rightarrow \boxed{x=80\;m};\\
\qquad \qquad \dfrac{y}{30}=\dfrac{180}{90} \Rightarrow 90\cdot y= 30 \cdot 180\Rightarrow \boxed{y=60\;m};\\
\qquad \qquad \dfrac{x}{20}=\dfrac{180}{90} \Rightarrow 90\cdot z= 20 \cdot 180\Rightarrow \boxed{z=40\;m}.[/tex]
Denotaremos por [tex]A_{M_{A}}[/tex], [tex]A_{M_{B}}[/tex] e [tex]A_{M_{C}}[/tex] as medidas das áreas das muretas dos terrenos [tex]\textbf{A, B}[/tex] e [tex]\textbf{C}[/tex], respectivamente. Notemos que essas áreas serão retângulos; assim:
[tex]\qquad A_{M_{A}}=80\cdot 0,5=40\;m^2.\\
\qquad A_{M_{B}}=60\cdot 0,4=24\;m^2.\\
\qquad A_{M_{C}}=40\cdot 0,6=24\;m^2.[/tex]
Finalizando, como o metro quadrado de mureta custa [tex]R\$\;10,00[/tex], seu João gastará [tex] \fcolorbox{black}{#eee0e5}{$(40+24+24)\cdot 10=880$}[/tex] reais com a construção das muretas dos três terrenos.
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
