Problema
Na figura, [tex]CA=CB[/tex] e [tex]CD=CE[/tex].
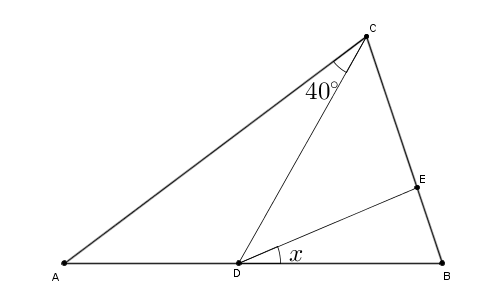
Calcule, em graus, a medida [tex]x[/tex] do ângulo [tex]EDB[/tex].
Solução 1
Vamos considerar [tex]\measuredangle{BAC} = \alpha[/tex] para obter alguns resultados preliminares que nos indicarão [tex] \measuredangle{DCE}[/tex].
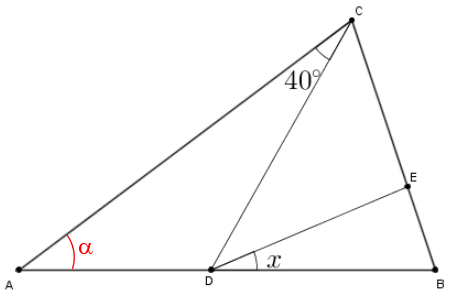
- Como [tex]CA = CB[/tex], o triângulo [tex]ABC[/tex] é isósceles de base [tex]AB[/tex], logo segue que [tex]\fbox{$\measuredangle{CBA} = \alpha$}[/tex].
- Como a soma dos ângulos internos de um triângulo é [tex]180^{\circ}[/tex], temos que [tex]\measuredangle{ADC} = 180^{\circ}-40^{\circ}-\alpha [/tex], ou seja [tex]\fbox{$\measuredangle{ADC}=140^{\circ}-\alpha$}[/tex].
- Também temos que
[tex]\qquad \measuredangle{CDE} = 180^{\circ}-\measuredangle{ADC}-x=180^{\circ}-(140^{\circ}-\alpha)-x[/tex]
e com isso [tex]\fbox{$\measuredangle{CDE} = 40^{\circ} + \alpha-x $}[/tex]. - Visto que [tex]\triangle{CDE}[/tex] é isósceles de base [tex]DE[/tex], concluímos que [tex]\fbox{$\measuredangle{CED}=\measuredangle{CDE} = 40^{\circ} + \alpha-x$}[/tex].
- E, finalmente,
[tex]\qquad \measuredangle{DCE} = 180^{\circ}-\measuredangle{CDE}-\measuredangle{CED}=180^{\circ}-2\cdot(40^{\circ} + \alpha-x)[/tex],
donde [tex]\fbox{$\measuredangle{DCE} = 100^{\circ}-2\alpha + 2x$} [/tex].
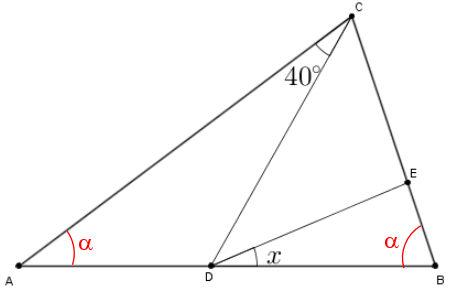
Agora, observe que [tex]\hat{A} + \hat{B} + \hat{C} = 180^{\circ}[/tex], ou seja, [tex]\alpha + \alpha +(40^{\circ} + 100^{\circ} – 2\alpha + 2x) = 180^{\circ}[/tex].
Simplificando essa igualdade, obtemos [tex]140^{\circ} + 2x = 180^{\circ}[/tex] e, consequentemente, a medida solicitada: [tex]\fcolorbox{black}{yellow}{$x= 20^{\circ}$}\,[/tex].
Solução elaborada pelo aluno do PIC-OBMEP Angelo Donizeti Lorenconi Junior, com contribuições dos Moderadores do Blog.
Solução 2
Pelo enunciado temos a seguinte figura:
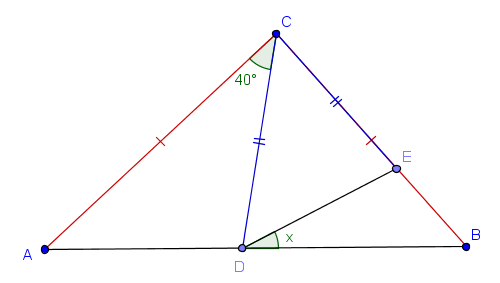
Suponhamos [tex]C\hat{A}B=\beta [/tex] e [tex] C\hat{D}E=\alpha[/tex].
- Veja que o [tex]\triangle ABC[/tex] é isósceles, logo [tex]C\hat{A}B=C\hat{B}A=\beta[/tex].
- Veja também que o [tex]\triangle CDE[/tex] é isósceles, logo [tex]C\hat{D}E=C\hat{E}D=\alpha[/tex].
- Notemos que [tex]A\hat{C}B=180-2\beta[/tex] e também [tex]A\hat{C}B=40+180-2\alpha [/tex].
Logo [tex]180-2\beta=40+180-2\alpha [/tex], ou seja,
[tex]\qquad \fbox{$\alpha=\beta + 20$}.\qquad\textcolor{#800000}{(i)}[/tex]
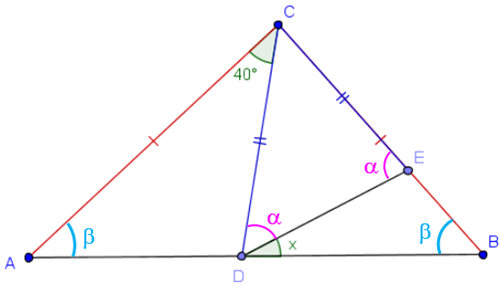
Observe que no triângulo [tex]\triangle DEB[/tex] temos que [tex]C\hat{B}D=\beta[/tex] e [tex]D\hat{E}B=180-\alpha[/tex]. Assim, como a soma das medidas dos ângulos internos do triângulo [tex]\triangle DEB[/tex] é [tex]180^{\circ}[/tex], teremos:
[tex]\quad\quad x+\beta+(180-\alpha)=180[/tex]
[tex]\quad\quad \fbox{$ x+\beta-\alpha=0$}. \qquad \textcolor{#800000}{(ii)}[/tex]
Substituindo [tex]\textcolor{#800000}{(i)}\,[/tex] em [tex]\,\textcolor{#800000}{(ii)}[/tex] segue que:
[tex]\quad\quad x+\beta-\left(\beta + 20 \right)=0[/tex]
[tex]\quad\quad x+\beta-\beta-20=0[/tex]
[tex]\quad\quad x-20=0[/tex],
donde [tex]\fcolorbox{black}{yellow}{$x= 20^{\circ}$}\,[/tex].
Solução elaborada pelo aluno do PIC-OBMEP William Zaniboni Silva, com contribuições dos Moderadores do Blog.
Solução 3
Sejam [tex]\measuredangle B\hat{A}C=a[/tex] e [tex]\measuredangle E\hat{D}C=b[/tex].
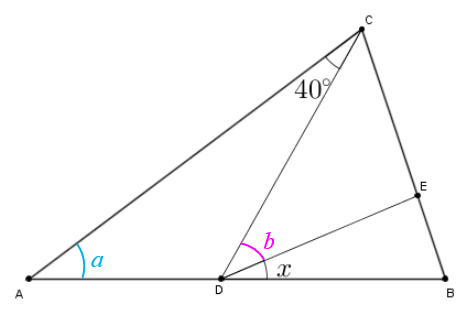
De acordo com o enunciado, [tex]CA=CB[/tex] e [tex]CD=CE[/tex]. Assim, [tex]\measuredangle B\hat{A}C= \measuredangle C\hat{B}A[/tex] e [tex]\measuredangle E\hat{D}C=\measuredangle C\hat{E}D[/tex].
Como a soma dos ângulos internos de um triângulo é igual a [tex]180^{\circ}[/tex], temos no triângulo [tex]ABC[/tex]:
[tex]\quad \quad \measuredangle B\hat{A}C + \measuredangle C\hat{B}A + \measuredangle A\hat{C}B = 180^{\circ}[/tex]
[tex]\quad \quad a+a + \measuredangle A\hat{C}B = 180^{\circ}[/tex]
[tex]\quad \quad 2a+ \measuredangle A\hat{C}B = 180^{\circ}.\qquad \textcolor{#800000}{(i)}[/tex]
Analogamente, no triângulo [tex]CDE[/tex], temos:
[tex]\quad \quad \measuredangle E\hat{D}C + \measuredangle C\hat{E}D + \measuredangle D\hat{C}E = 180^{\circ}[/tex]
[tex]\quad \quad b+b+\measuredangle D\hat{C}E = 180^{\circ}[/tex]
[tex]\quad \quad 2b+\measuredangle D\hat{C}E = 180^{\circ}.\qquad \textcolor{#800000}{(ii)}[/tex]
Por outro lado, note que [tex]\measuredangle A\hat{C}B=\measuredangle D\hat{C}E+40^{\circ}[/tex]; assim,
[tex]\quad \quad \measuredangle D\hat{C}E=\measuredangle A\hat{C}B-40^{\circ}[/tex].
Substituindo essa expressão em [tex]\textcolor{#800000}{(ii)}[/tex] obtemos que
[tex]\quad \quad 2b+\measuredangle A\hat{C}B-40^{\circ}=180^{\circ}.\qquad \textcolor{#800000}{(iii)}[/tex]
Igualando [tex]\textcolor{#800000}{(i)}[/tex] e [tex]\textcolor{#800000}{(iii)}[/tex] segue que
[tex]\quad \quad 2a+\measuredangle A\hat{C}B=2b+\measuredangle A\hat{C}B-40^{\circ}[/tex]
[tex]\quad \quad 2a=2b-40^{\circ}[/tex]
[tex]\quad \quad a=b-20^{\circ}.[/tex]
Olhando para o triângulo [tex]BED[/tex], temos:
[tex]\quad \quad \measuredangle B\hat{D}E + \measuredangle E\hat{B}D + \measuredangle D\hat{E}B = 180^{\circ}[/tex]
[tex]\quad \quad x+a+(180^{\circ}-b)=180^{\circ}.[/tex]
Substituindo [tex]a[/tex] por [tex]b-20^{\circ}[/tex]:
[tex]\quad \quad x+(b-20^{\circ})+(180^{\circ}-b)=180^{\circ}[/tex]
[tex]\quad \quad x+b-b-20^{\circ}+180^{\circ}=180^{\circ}[/tex];
logo, [tex]\fcolorbox{black}{yellow}{$x= 20^{\circ}$}\,[/tex].
Solução elaborada pelo aluno do PIC-OBMEP Paulo Ricardo Souza Rodrigues, com contribuições dos Moderadores do Blog.
