✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 6º ano do E. F. – Nível de dificuldade: Fácil)
(OPM, 2014 – Adaptado) Um grupo de alpinistas escolheu o desenho mostrado na figura abaixo para imprimir nas camisetas que utilizarão na próxima escalada que farão.
Sobre um dos lados de um quadrado, foram pintados dois triângulos marrons iguais, de lados todos iguais, unidos por um de seus vértices. A parte do quadrado que sobrou foi pintada de azul, para simbolizar o céu, e tem perímetro igual a [tex]120\, \text{cm}[/tex].

Qual a área total do desenho a ser pintado em cada camiseta?
Solução 1
Observe que o perímetro da região do desenho que foi pintada de azul é constituído por três lados do quadrado e quatro lados dos triângulos.
Mas dois lados dos triângulos têm o mesmo comprimento de um lado do quadrado; assim, a medida do perímetro da figura azul é igual a cinco vezes o comprimento de um lado do quadrado. Com isso, como a figura azul tem perímetro igual a [tex]120\, \text{cm}[/tex], cada lado do quadrado mede [tex]\dfrac{120}{5}=\boxed{24\, \text{cm}}.[/tex]
Portanto, a medida da área do quadrado é igual a [tex]24^2=\, \fcolorbox{black}{#eee0e5}{$576\, \, \text{cm}^2$}\, .[/tex]
Solução elaborada pelos Moderadores do Blog.
Solução 2
(Indicada a partir do 7º ano do E. F.)
Poderíamos ter resolvido o problema utilizando equações explicitamente. Vamos fazê-lo a partir da medida do lado do triângulo.
Observe que o perímetro da região do desenho que foi pintada de azul é constituído por três lados do quadrado e quatro lados dos triângulos.
Mas cada lado do quadrado tem o mesmo comprimento que dois lados dos triângulos; assim, a medida do perímetro da figura azul é igual a dez vezes o comprimento de um lado dos triângulos. Vamos, então, supor que o comprimento em centímetros de cada lado dos triângulos seja [tex]x[/tex].
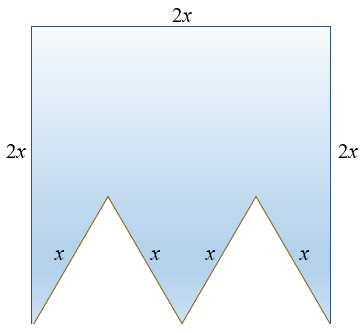
Com isso, como a figura azul tem perímetro igual a [tex]120\, \text{cm}[/tex], cada lado do triângulo mede
[tex]\qquad x=\dfrac{120}{10}=\boxed{12\, \text{cm}}[/tex]
e, assim, o comprimento de cada lado do quadrado é
[tex]\qquad 2 \times 12=\boxed{24\, \text{cm}}.[/tex]
Portanto, a medida [tex]S[/tex] da área do quadrado é igual a:
[tex]\qquad S=24^2=\, \fcolorbox{black}{#eee0e5}{$576\, \, \text{cm}^2$}\, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
