.Problema para ajudar na escola: Desenhando com Tangram

Problema
(A partir do 6º ano do E. F. – Nível de dificuldade: Médio)

(PUC-SP, 2010 – Adaptado) O Tangram é um antigo quebra-cabeça chinês cujo nome significa “sete tábuas da sabedoria”. Ele é composto de sete peças — cinco triângulos isósceles, um paralelogramo e um quadrado — que podem ser posicionadas de modo a formar um quadrado, como é mostrado na figura abaixo.

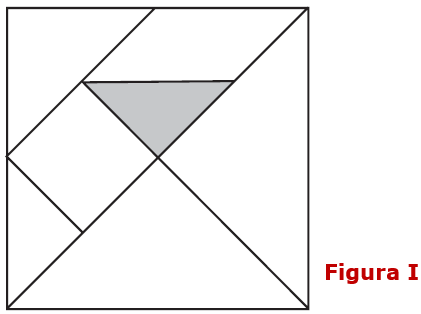
Utilizando seis das peças de um Tangram, foi construída a seta mostrada na figura a seguir.

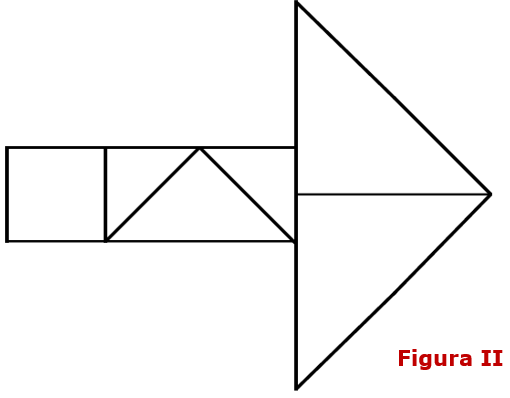
Sabendo que a área do triângulo sombreado na Figura I é igual a [tex]9\, cm^2[/tex], qual é a área, em centímetros quadrados, da superfície da seta exibida na Figura II ?

Solução

Vamos dividir o quadrado que origina as peças do Tangram em dezesseis triângulos congruentes ao triângulo sombreado de cinza na Figura I . Para facilitar a identificação das sete peças, colorimos cada uma de uma cor.

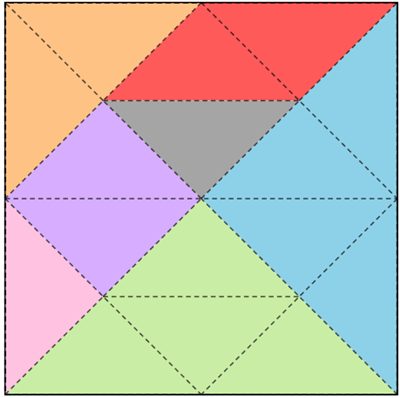
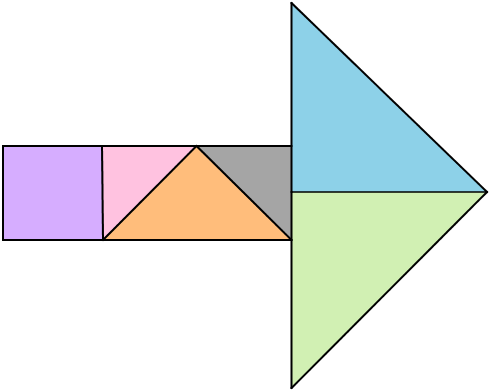
Observando as figuras acima, vemos que apenas o paralelogramo vermelho não foi utilizado para construir a seta. Assim, a área da superfície da seta é equivalente à área do quadrado que originou as peças do Tangram menos a área do paralelogramo vermelho e a área deste é equivalente à área de dois triângulos sombreados de cinza.
Dessa forma, a seta é equivalente a quatorze triângulos sombreados de cinza. Fazendo as continhas, como a área do triângulo sombreado na Figura I é igual a [tex]9\, cm^2[/tex], se [tex]S[/tex] é a medida da área da seta, segue que:
[tex]\qquad S=14 \times 9\\
\qquad \, \fcolorbox{black}{#eee0e5}{$S=126\, cm^2$}\, .[/tex]

Solução elaborada pelos Moderadores do Blog.

Um applet para se divertir

Você pode utilizar o applet abaixo para construir a flecha a partir do quadrado, ambos coloridos de acordo com a solução do problema!
Instruções:
(1) Espere o applet carregar. (O aplicativo pode demorar um pouquinho para carregar.)
(2) Para transladar qualquer uma das peças do Tangram, clique sobre a peça, mantenha o mouse pressionado e arraste-a suavemente. (Se você estiver utilizando um celular ou um tablet, toque levemente na peça e movimente-a.)
(3) Para rodar uma peça, clique sobre o vértice da peça identificado com um pequeno círculo, mantenha o mouse pressionado e rode-a suavemente. (Se você estiver utilizando um celular ou um tablet, toque levemente no ponto e movimente-o.)
(4) Você poderá fazer movimentos “mais finos” das peças utilizando o teclado do seu computador. Para isso:
– para transladar uma peça, clique sobre ela com o botão esquerdo do mouse; em seguida, mantendo a tecla Shift do teclado apertada, faça os movimentos utilizando as teclas “mover para direita” ou “mover para esquerda” ou “mover para cima” ou “mover para baixo” .
– para rodar uma peça, clique sobre sobre o vértice com um pequeno círculo, usando o botão esquerdo do mouse; em seguida, mantendo a tecla Shift do teclado apertada, faça os movimentos utilizando as teclas “mover para direita” ou “mover para esquerda” ou “mover para cima” ou “mover para baixo” (dependendo da posição da peça, nem todas as teclas produzem o efeito de rotação).
(5) Se quiser voltar para a visualização inicial, clique nas setinhas circulares que aparecem no canto superior direito do aplicativo.

OBMEP_ srdg, criado com o GeoGebra