Problema
(Indicado a partir do 8º ano do E. F.)
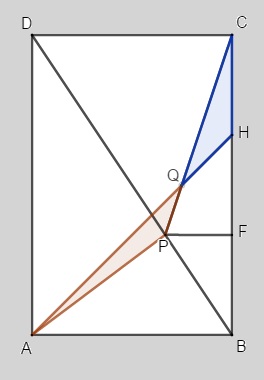
(Adaptado do livro Círculos Matemáticos) Considere o retângulo [tex]ABCD[/tex]. Sejam [tex]P[/tex] um ponto na diagonal [tex]BD[/tex] e [tex]F[/tex] um ponto sobre o lado [tex]BC[/tex] tais que o segmento [tex]PF[/tex] é paralelo ao lado [tex]AB[/tex]. Sendo [tex]H[/tex] um ponto do lado [tex]BC[/tex] tal que [tex]\overline{BF}=\overline{FH}[/tex] e [tex]Q[/tex] o ponto de interseção dos segmentos [tex]PC[/tex] e [tex]AH[/tex], mostre que os triângulos [tex]\Delta APQ[/tex] e [tex]\Delta CHQ[/tex] possuem a mesma área.

Lembrete e notações
(1) Caso de congruência L.L.L. (lado – lado- lado): Se dois triângulos têm ordenadamente congruentes os três lados, então estes triângulos são congruentes.
(2) Caso de congruência L.A.L. (lado – ângulo – lado): Se dois triângulos têm ordenadamente congruentes dois lados e o ângulo por eles definido, então estes triângulos são congruentes.
✐ Se você não se lembra desses casos de congruência entre triângulos, clique AQUI.
Notações: Denotaremos o segmento formado pelos pontos [tex]X[/tex] e [tex]Y[/tex] por [tex]XY[/tex] e sua medida por [tex]\overline{XY}[/tex]; o triângulo formado pelos pontos [tex]X, Y[/tex] e [tex]Z[/tex] por [tex]\Delta XYZ[/tex] e sua área por [tex]S(\Delta XYZ)[/tex]; a medida do ângulo formado pelos pontos [tex]X, Y[/tex] e [tex]Z[/tex] com vértice em [tex]Y[/tex] por [tex]X\widehat{Y}Z[/tex].
Solução
Na figura fornecida no problema, traçamos os segmentos [tex]AC[/tex] e [tex]PH[/tex].
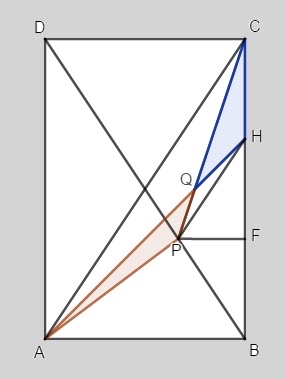
Como o ponto [tex]F[/tex] é o ponto médio do segmento [tex]BH[/tex] e o segmento [tex]PF[/tex] é perpendicular ao lado [tex]BC[/tex], concluímos que os triângulos [tex]\Delta PFH[/tex] e [tex]\Delta PFB[/tex] são congruentes (pelo caso [tex]LAL[/tex]) e, portanto, [tex]\Delta PBH[/tex] é um triângulo isósceles. Então,
[tex]P\widehat{H}B=P\widehat{B}H=D\widehat{B}C. \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \textcolor{#800000}{(i)}[/tex]
Vemos que os triângulos [tex]\Delta ACB[/tex] e [tex]\Delta DBC[/tex] são congruentes (pelo caso [tex]LLL[/tex]); logo,
[tex]D\widehat{B}C=A\widehat{C}B. \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \textcolor{#800000}{(ii)}[/tex]
Da igualdades [tex]\textcolor{#800000}{(i)}[/tex] e [tex]\textcolor{#800000}{(ii)}[/tex], segue que [tex]P\widehat{H}B=A\widehat{C}B.[/tex] Com isso, temos que os segmentos [tex]PH[/tex] e [tex]AC[/tex] são paralelos.
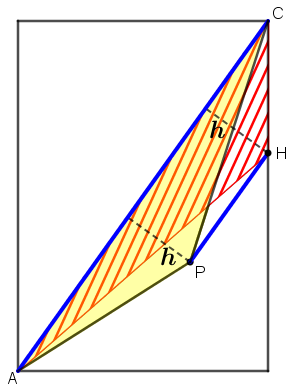
Dessa forma, [tex]S(\Delta APC)=S(\Delta ACH)[/tex], considerando as bases dos triângulos o lado comum [tex]AC[/tex]. Para entender melhor essa afirmação, veja a figura abaixo, na qual mantivemos no interior do retângulo [tex]ABCD[/tex] apenas os elementos geométricos que sustentam a afirmação. Observe que, devido ao paralelismo dos segmentos [tex]PH[/tex] e [tex]AC[/tex], o comprimento das alturas dos triângulos [tex]\Delta ACH[/tex] e [tex]\Delta ACH[/tex] relativas à base comum [tex]AC[/tex] é o mesmo, o que garante que esses triângulos, de fato, têm a mesma área.
Agora, observando a figura do início da solução, notamos que
\begin{equation}
S(\Delta APC)-S(\Delta AQC)=S(\Delta ACH)-S(\Delta AQC). \end{equation}
Portanto, [tex]S(\Delta APQ)=S(\Delta CHQ)[/tex], ou seja, os triângulos [tex]\Delta APQ[/tex] e [tex]\Delta CHQ[/tex] têm a mesma área.
Solução elaborada pelos Moderadores do Blog.
