Problema
(Indicado a partir do 9º ano do E. F.)
Uma formiga está no centro de uma das faces de um cubo e, na face oposta, existe um torrão de açúcar localizado em um de seus vértices. Sabendo que a aresta do cubo mede [tex]10 \, cm[/tex], qual o comprimento do caminho mais curto que a formiga deve seguir até o torrão?
Solução
Desenho ilustrativo da situação e da planificação do cubo.
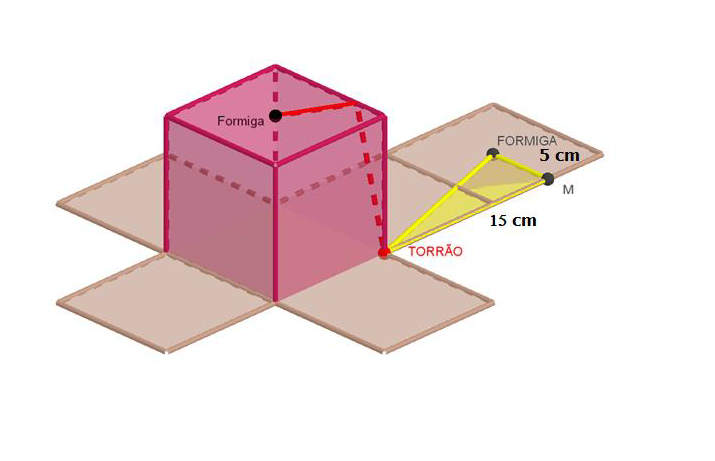
Perceba que a formiga deverá, na realidade, sair do centro de um quadrado e atravessar outro quadrado até seu vértice, conforme fica claro na planificação, já que a menor distância entre dois pontos é dada pelo segmento de reta que estes definem.
Assim, a formiga deve seguir o trajeto [tex]\overline{FT}[/tex] da figura, sendo [tex]F[/tex] e [tex]T[/tex] os pontos nos quais se localizam a formiga e o torrão, respectivamente.
Aplicando o Teorema de Pitágoras no triângulo [tex]FMT[/tex], temos:
[tex]\qquad (FT)^2 = 15^2 + 5^2[/tex]
[tex]\qquad (FT)^2 = 250[/tex]
[tex]\qquad FT = \sqrt{250}[/tex]
[tex]\qquad FT = 5\sqrt{10}.[/tex]
Portanto, o menor percurso que a formiga deve fazer até o torrão será de [tex] \, \fcolorbox{black}{#eee0e5}{$5\sqrt{10} \approx 15,8 \, cm$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
