Problema
(Indicado a partir do 8º ano do E. F.)
Na figura abaixo, [tex]ABCD[/tex] é um quadrilátero cujos lados [tex]\overline{AD}[/tex] e [tex]\overline{BC}[/tex] têm o mesmo comprimento e a medida dos ângulos [tex]D\hat{A}B [/tex] e [tex]C\hat{B}A[/tex] são [tex]80^\circ[/tex] e [tex]40^\circ[/tex], respectivamente. O ponto [tex]P[/tex] é tal que o triângulo [tex]DPC[/tex] é equilátero.
Calcule o perímetro do triângulo [tex]APB[/tex], sabendo que o comprimento do segmento [tex]\overline{AB}[/tex] é [tex]6\;cm[/tex].
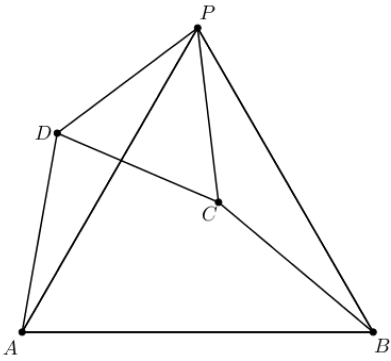
Notação: Denotaremos o segmento definido por dois pontos, digamos [tex]A[/tex] e [tex]B[/tex], por [tex]\overline{AB}[/tex] e o seu comprimento por [tex]AB[/tex].

Lembretes
(1) A soma dos ângulos internos de qualquer triângulo vale [tex]180^\circ[/tex].
(2) A soma dos ângulos internos de qualquer quadrilátero convexo vale [tex]360^\circ[/tex].
(3) Se dois triângulos possuem dois lados congruentes e os ângulos entre esses lados possuem a mesma medida, então esses triângulos são congruentes pelo caso L.A.L. .
(4) Se um triângulo isósceles possui um ângulo de [tex]60^\circ[/tex], então esse triângulo é equilátero.
Solução
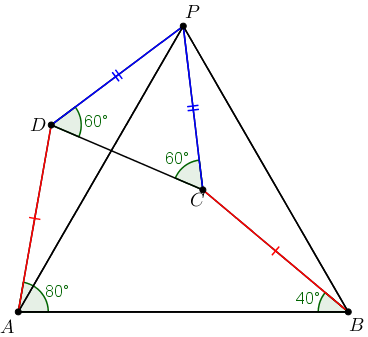
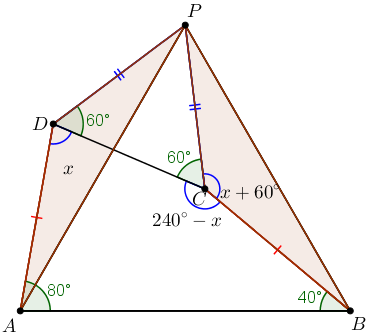
Inicialmente, vamos destacar na figura a seguir as informações dadas no enunciado:
I) [tex]AD = BC[/tex];
II) a medida do ângulo [tex]D\hat{A}B [/tex] é [tex]80^\circ[/tex];
III) a medida do ângulo [tex]C\hat{B}A [/tex] é [tex]40^\circ[/tex];
IV) [tex]DPC[/tex] é um triângulo equilátero. Dessa afirmação, concluímos que [tex]P\hat{D}C[/tex] e [tex]P\hat{C}D[/tex] medem [tex]\dfrac{180^\circ}{3}=60^\circ.[/tex]
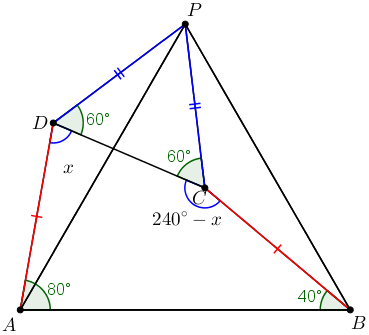
Chamemos de [tex]x[/tex] a medida em graus do ângulo [tex]A\hat{D}C[/tex]. Pelo lembrete 2, podemos concluir que a medida do ângulo [tex]D\hat{C}B[/tex] é:
[tex]\qquad \qquad 360^\circ-80^\circ-40^\circ-x=\boxed{240^\circ-x} \, .[/tex]
Como um ângulo de uma volta completa mede [tex]360^\circ[/tex], podemos encontrar a medida do ângulo [tex]P\hat{C}B[/tex] em função de [tex]x[/tex]:
[tex]\qquad \qquad 360^\circ-60^\circ-(240^\circ-x)=\boxed{60^\circ+x} \, .[/tex]
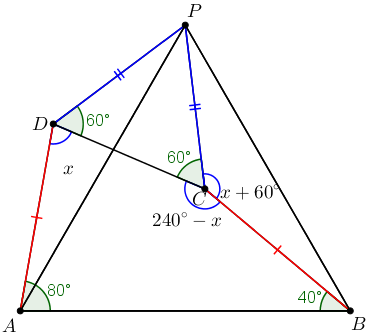
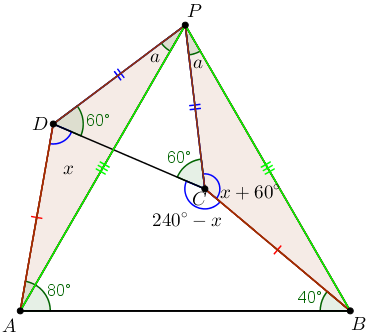
Perceba que o triângulo [tex]PDA[/tex] é congruente ao triângulo [tex]PCB[/tex], pelo caso L.A.L. .
Devido a essa congruência, os segmentos [tex]\overline{PA}[/tex] e [tex]\overline{PB}[/tex] têm o mesmo comprimento e os ângulos [tex]D\hat{P}A[/tex] e [tex]C\hat{P}B[/tex] também têm a mesma medida, digamos [tex]a.[/tex]
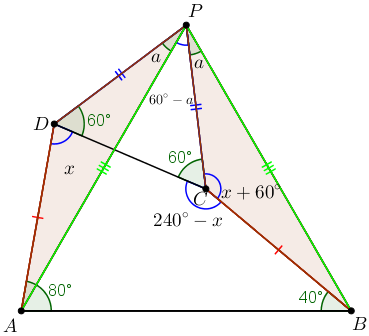
Como o triângulo [tex]DPC[/tex] é equilátero, o ângulo [tex]A\hat{P}C[/tex] mede [tex]60^\circ -a[/tex].
Note que o triângulo [tex]APB[/tex] é isósceles e o ângulo [tex]A\hat{P}B[/tex] mede [tex]60^\circ[/tex]. Assim, pelo lembrete 4, o triângulo [tex]APB[/tex] é equilátero.
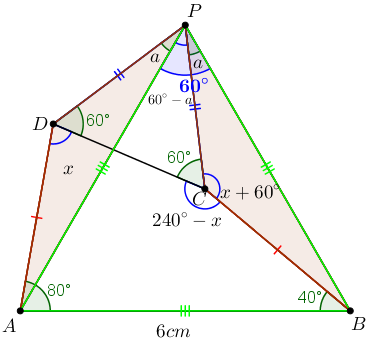
Como [tex]AB = 6\; cm[/tex], o perímetro do triângulo será [tex]6+6+6=\fcolorbox{black}{#eee0e5}{$18\;cm$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
