Problema
(Indicado a partir do 9º ano do E. F.)
As duas polias com centros em [tex]C[/tex] e [tex]D[/tex] mostradas na figura possuem raios que medem, respectivamente, [tex]8[/tex] cm e [tex]3[/tex] cm e a distância entre seus centros é [tex]13[/tex] cm.
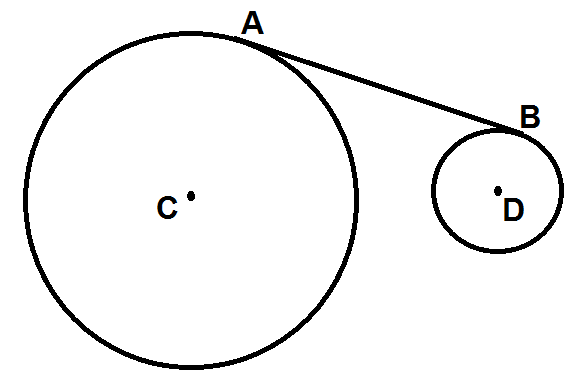
Se [tex]A[/tex] e [tex]B[/tex] são pontos de tangência da correia que envolve as roldanas, determine a medida da distância entre [tex]A[/tex] e [tex]B[/tex].

Lembretes
(1) Uma reta tangente a uma circunferência é perpendicular ao raio no seu ponto de tangência.
(2) Os lados opostos de um paralelogramo têm a mesma medida.
(3) Teorema de Pitágoras: Em um triângulo retângulo, o quadrado da hipotenusa é a soma dos quadrados dos catetos.
Solução
Ligando [tex]C[/tex] a [tex]A[/tex] e [tex]D[/tex] a [tex]B[/tex], obtemos dois segmentos paralelos, uma vez que, pelo Lembrete 1, ambos são perpendiculares a [tex]\overline{AB} \, .[/tex]
Agora, traçando o segmento [tex]\overline{BE}[/tex] paralelo ao segmento [tex]\overline{CD}[/tex], obtemos um triângulo retângulo [tex]ABE[/tex].
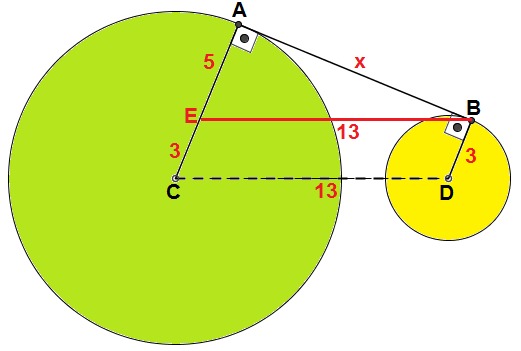
Após isso, perceba que [tex]CEBD[/tex] é paralelogramo, pois os lados opostos são paralelos. Assim, pelo Lembrete 2, [tex]\overline{DB}[/tex] e [tex]\overline{CE}[/tex] medem [tex]3[/tex] cm e [tex]\overline{CD}[/tex] e [tex]\overline{EB}[/tex] medem [tex]13[/tex] cm. Observe também que [tex]\overline{EA}[/tex] mede [tex]5[/tex] cm, já que o raio da polia maior mede [tex]8[/tex] cm.
Finalmente, se [tex]x[/tex] denotar o comprimento em centímetros de [tex]\overline{AB}[/tex], aplicando o Teorema de Pitágoras, Lembrete 3, ao triângulo [tex]ABE[/tex], vem que:
[tex]\qquad 13^2=5^2+x^2[/tex]
[tex]\qquad x^2=144[/tex]
[tex]\qquad x=12[/tex], já que [tex]x \gt 0.[/tex]
Portanto, a distância entre os pontos [tex]A[/tex] e [tex]B[/tex] é [tex] \, \fcolorbox{black}{#eee0e5}{$12 \, cm$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
