Problema
(Indicado a partir do 9º ano do E. F.)
Observe a figura a seguir.
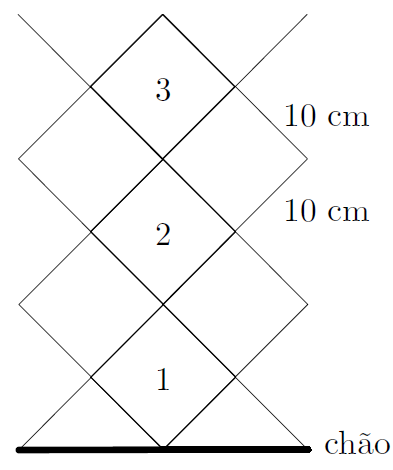
Podemos observar a representação de três níveis de grade de uma cerca quadriculada cujos quadradinhos têm lados de [tex]10[/tex] cm. No total, essa cerca é composta por [tex]20[/tex] níveis iguais aos que foram representados acima. Qual a altura aproximada, em metros, dessa cerca de [tex]20[/tex] níveis? (Dado: [tex]\sqrt{2}=1,4[/tex].)
(Extraído do Seletivo de Admissão à Escola de Aprendizes Marinheiros, 2011/2012)
Solução
A altura total da cerca de [tex]20[/tex] níveis será [tex]20[/tex] vezes a diagonal de um quadrado de lado [tex]10\,cm[/tex] e podemos utilizar o Teorema de Pitágoras para obter o comprimento [tex]d[/tex] dessa diagonal:
[tex]\qquad d^2=10^2+10^2\\
\qquad d^2=200\\
\qquad d=\sqrt{200}[/tex] (Utilizamos apenas a raiz positiva, pois [tex]d[/tex] é um comprimento)
[tex]\qquad d=10\sqrt{2} \, cm.[/tex]
Desta forma, se [tex]h[/tex] for a altura da cerca, segue que:
[tex]\qquad h= 20 \cdot 10\sqrt{2}=280 \, cm[/tex],
ou seja, a altura aproximada, em metros, dessa cerca é [tex] \, \fcolorbox{black}{#eee0e5}{$2,8 \, m$} \, .[/tex]
Na conversão de centímetros ([tex]cm[/tex]) para metros ([tex]m[/tex]), o esqueminha abaixo pode ajudar!
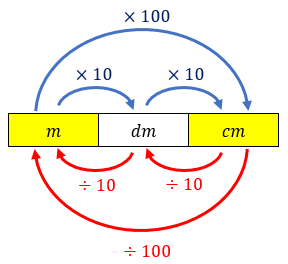
Solução elaborada pelos Moderadores do Blog.
