.Problemão: Somar e Multiplicar

Problema
(Indicado a partir do 2º ano do E. M.)

Qual o valor da expressão [tex] \boxed{1 \cdot 2 \cdot 3 +2 \cdot 3 \cdot 4 + 3 \cdot 4 \cdot 5 + … + 98 \cdot 99 \cdot 100}[/tex]?

Ajuda

explicador_p

As duas soluções que apresentaremos para este problema utilizam propriedades dos coeficientes binomiais que podem ser visualizadas no Triângulo de Pascal. Elas serão apresentadas e ilustradas neste Lembrete.

Propriedade 1: Sejam [tex]k[/tex] e [tex]t[/tex] números naturais não nulos. Então:

[tex] \qquad \qquad \begin{pmatrix} k \\ k \end{pmatrix} + \begin{pmatrix} k + 1 \\ k \end{pmatrix} + \begin{pmatrix} k + 2 \\ k \end{pmatrix} + … + \begin{pmatrix} k + t \\ k \end{pmatrix} = \begin{pmatrix} k + t + 1 \\ k + 1 \end{pmatrix} [/tex]

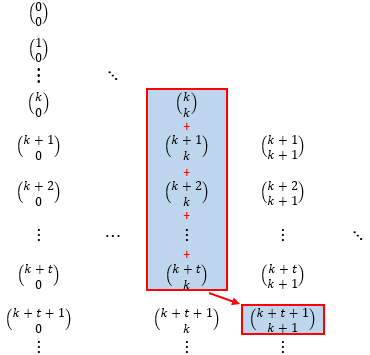
Esta propriedade é conhecida como Teorema das Colunas do Triângulo de Pascal, pois ela pode ser enunciada a partir do Triângulo de Pascal da seguinte forma:

A soma dos primeiros elementos de uma coluna do Triângulo de Pascal é igual ao elemento que está na linha seguinte e na coluna seguinte da última parcela da soma.(*)

Propriedade 2: Relação de Stifel – Sejam [tex]k[/tex] e [tex]t[/tex] números naturais não nulos. Então:

[tex] \qquad \qquad \begin{pmatrix} k \\ t \end{pmatrix} + \begin{pmatrix} k \\ t+1 \end{pmatrix} = \begin{pmatrix} k+1 \\ t+1 \end{pmatrix} [/tex].

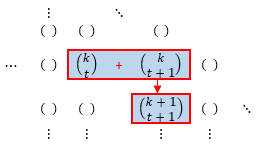
Esta propriedade também pode ser enunciada a partir do Triângulo de Pascal da seguinte forma:

Somando dois elementos consecutivos de uma mesma linha obtém-se o elemento situado abaixo da segunda parcela.(*)

Para relembrar um pouco sobre coeficientes binomiais e
sobre o Triângulo de Pascal, clique no botão abaixo.

Para [tex]n[/tex] e [tex]r[/tex] números naturais tais que [tex]0\leqslant r \leqslant n[/tex], chamamos de coeficiente binomial ou número binomial o quociente denotado por [tex]\dbinom{n}{r}[/tex] e assim definido: [tex]\boxed{\dbinom{n}{r}=\dfrac{n!}{(n-r)! \, r!}}[/tex]. (Em se tratando de fatoriais, é sempre bom se lembrar de que [tex]0!=1[/tex].)
Nesta nossa breve discussão, no número binomial [tex]\dbinom{n}{r}[/tex], denominaremos [tex]n[/tex] de índice superior e [tex]r[/tex] de índice inferior.
Se [tex]n[/tex] e [tex]r[/tex] são números naturais tais que [tex]0\leqslant r \leqslant n[/tex], chamamos de Triângulo de Pascal ao triângulo numérico infinito formado por coeficientes binomiais [tex]\dbinom{n}{r}[/tex] dispostos em linhas e colunas de forma que:

números binomiais que tenham o mesmo índice superior fiquem na mesma linha linha, ordenados sequencialmente pelos índices inferiores e
números binomiais que tenham o mesmo índice inferior fiquem na mesma coluna, ordenados sequencialmente pelos índices superiores.

[tex]\textcolor{#800000}{\dbinom{0}{0}\\
\dbinom{1}{0} \dbinom{1}{1}\\
\dbinom{2}{0} \dbinom{2}{1} \dbinom{2}{2}\\
\dbinom{3}{0} \dbinom{3}{1} \dbinom{3}{2}\dbinom{3}{3}\\
\dbinom{4}{0} \dbinom{4}{1} \dbinom{4}{2}\dbinom{4}{3}\dbinom{4}{4}}\\
\qquad \qquad \quad \vdots\\
\textcolor{#800000}{\dbinom{n}{0} \dbinom{n}{1} \dbinom{n}{2}\dbinom{n}{3} \dbinom{n}{4} \cdots \dbinom{n}{n}}\\
\qquad \qquad \quad \vdots\\
[/tex]

Observe que cada linha do Triângulo de Pascal possui uma quantidade finita de elementos, mas as colunas do Triângulo possuem uma quantidade infinita de elementos.
Se for conveniente, podemos escrever o Triângulo de Pascal substituindo cada coeficiente binomial por seu respectivo valor ou até mesmo dispor os números binomiais de forma a obter uma formação diferente do Triângulo.
Veja o Triângulo de Pascal com os coeficientes binomiais que definem as sete primeiras linhas calculados e visualizado nas duas formas mais utilizadas:

[tex]
\textcolor{#800000}{1 \, \\
1 \, \quad 1 \, \\
1 \, \quad 2 \, \quad 1 \, \\
1 \, \quad 3 \, \quad 3 \, \quad \, 1 \, \\
1 \, \quad 4 \, \quad 6 \, \quad \, 4 \, \quad \, 1 \, \\
1 \, \quad 5 \, \quad 10 \quad 10 \quad 5 \, \quad \, 1\\
1 \, \quad 6 \, \quad 15 \quad 20 \quad 15 \quad 6 \quad \, 1\\
1 \, \quad 7 \, \quad 21 \quad 35 \quad 35 \quad 21 \quad 7 \quad 1}\\
\qquad \qquad \quad \vdots [/tex]

\begin{equation}\textcolor{#800000}{1 \, \\
1 \, \quad \, 1 \, \\
1 \, \quad \, 2 \, \quad \, 1 \, \\
1 \, \quad \, 3 \, \quad \, 3 \, \quad \, 1 \, \\
1 \, \quad \, 4 \, \quad \, 6 \, \quad \, 4 \, \quad \, 1 \, \\
1 \, \quad \, 5 \, \quad \, 10 \, \quad \, 10 \, \quad \, 5 \, \quad \, 1 \, \\
1 \, \quad \, 6 \, \quad \, 15 \, \quad \, 20 \, \quad \, 15 \, \quad \, 6 \, \quad \, 1 \, \\
1 \, \quad \, 7 \, \quad \, 21 \, \quad \, 35 \, \quad \, 35 \, \quad \, 21 \, \quad \, 7 \, \quad 1}\\
\vdots \end{equation}

(*) Tenham em conta que a maneira diferente de escrevermos as Propriedades 1 e 2 não são demonstrações e nem justificativas para elas.

Solução 1

Solução elaborada pelos Moderadores do Blog.

Solução 2

Se [tex] x = 1\cdot2\cdot3 + 2\cdot3\cdot4 + 3\cdot4\cdot5 + … + 98\cdot99\cdot100[/tex], então:
[tex] \qquad \dfrac{x}{3!} = \dfrac{1\cdot2\cdot3}{3!} + \dfrac{2\cdot3\cdot4}{3!} + \dfrac{3\cdot4\cdot5}{3!} + … + \dfrac{98\cdot99\cdot100}{3!}.\qquad \textcolor{#800000}{(i)} [/tex]
Da definição de número binomial, tem-se que [tex] \begin{pmatrix} n \\ p \end{pmatrix} = \dfrac{n!}{(n-p)!\cdot p!} [/tex]; logo, da expressão [tex] \textcolor{#800000}{(i)} [/tex], segue que:
[tex]\qquad \dfrac{x}{3!} = \begin{pmatrix} 3 \\ 3 \end{pmatrix} + \begin{pmatrix} 4 \\ 3 \end{pmatrix} + \begin{pmatrix} 5 \\ 3 \end{pmatrix} + … + \begin{pmatrix} 100 \\ 3 \end{pmatrix}.\qquad \textcolor{#800000}{(ii)} [/tex]
Pela relação de Stifel, temos que
[tex] \qquad \begin{pmatrix} k \\ t \end{pmatrix} = \begin{pmatrix} k+1 \\ t+1 \end{pmatrix}-\begin{pmatrix} k \\ t+1 \end{pmatrix} [/tex],
assim, podemos reescrever os termos da expressão [tex] \textcolor{#800000}{(ii)} [/tex] nas seguintes formas:
[tex] \qquad \begin{pmatrix} 4 \\ 3 \end{pmatrix} = \begin{pmatrix} 5 \\ 4 \end{pmatrix}-\begin{pmatrix} 4 \\ 4 \end{pmatrix} [/tex]
[tex]\qquad \begin{pmatrix} 5 \\ 3 \end{pmatrix} = \begin{pmatrix} 6 \\ 4 \end{pmatrix}-\begin{pmatrix} 5 \\ 4 \end{pmatrix} [/tex]
[tex]\qquad \begin{pmatrix} 6 \\ 3 \end{pmatrix} = \begin{pmatrix} 7 \\ 4 \end{pmatrix}-\begin{pmatrix} 6 \\ 4 \end{pmatrix} [/tex]
[tex]\qquad \begin{pmatrix} 7 \\ 3 \end{pmatrix} = \begin{pmatrix} 8 \\ 4 \end{pmatrix}-\begin{pmatrix} 7 \\ 4 \end{pmatrix} [/tex]
[tex]\qquad \qquad \vdots[/tex]
[tex]\qquad \begin{pmatrix} 100 \\ 3 \end{pmatrix}= \begin{pmatrix} 101 \\ 4 \end{pmatrix}-\begin{pmatrix} 100 \\ 4 \end{pmatrix} [/tex].
Somando membro a membro as igualdades acima podemos cancelar os vários termos semelhantes opostos (observe que cada minuendo é cancelado com o subtraendo da diferença seguinte) e obter:
[tex] \qquad \begin{pmatrix} 4 \\ 3 \end{pmatrix} + \begin{pmatrix} 5 \\ 3 \end{pmatrix} + … + \begin{pmatrix} 100 \\ 3 \end{pmatrix} = \begin{pmatrix} 101 \\ 4 \end{pmatrix}-\begin{pmatrix} 4 \\ 4 \end{pmatrix} [/tex].
Como [tex] \begin{pmatrix} 4 \\ 4 \end{pmatrix} = \begin{pmatrix} 3 \\ 3 \end{pmatrix} = 1 [/tex], teremos que:
[tex] \qquad \begin{pmatrix} 3 \\ 3 \end{pmatrix} + \begin{pmatrix} 4 \\ 3 \end{pmatrix} + \begin{pmatrix} 5 \\ 3 \end{pmatrix} + … + \begin{pmatrix} 100 \\ 3 \end{pmatrix} = \begin{pmatrix} 101 \\ 4 \end{pmatrix} [/tex].
Assim, segue que:
[tex]\qquad x = 3!\cdot \begin{pmatrix} 101 \\ 4 \end{pmatrix} \\
\qquad x = 3! \cdot \dfrac{101!}{97! \cdot 4!} \\
\qquad x = \dfrac{101!}{97! \cdot 4}\\
\qquad x = \dfrac{101\cdot 100 \cdot 99 \cdot 98}{4}\\
\qquad x = 24497550 [/tex]
e, portanto, [tex] \, \fcolorbox{black}{#eee0e5}{$1 \cdot 2 \cdot 3 +2 \cdot 3 \cdot 4 + 3 \cdot 4 \cdot 5 + … + 98 \cdot 99 \cdot 100=24 \, 497 \, 550$} \, .[/tex]

Solução elaborada pelos Moderadores do Blog.