Problema
(Indicado a partir do 2º ano do E. M.)
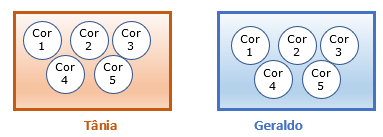
(FGV, 2013) Tânia e Geraldo têm, cada um, uma urna contendo cinco bolas. Cada urna contém uma bola de cada uma das seguintes cores: azul, verde, preta, branca e roxa. As bolas são distinguíveis umas das outras apenas por sua cor. Tânia transfere, ao acaso, uma bola da sua urna para a de Geraldo. Em seguida, Geraldo transfere, ao acaso, uma bola da sua urna para a de Tânia.
Ao final das transferências, qual a probabilidade de que as duas urnas tenham sua configuração inicial?
Solução
Sabemos que as bolas são distinguíveis umas das outras apenas pela cor.
Depois de Tânia transferir uma bola da sua urna para a urna de Geraldo, a urna dele ficará com [tex]6[/tex] bolas, sendo duas da mesma cor.
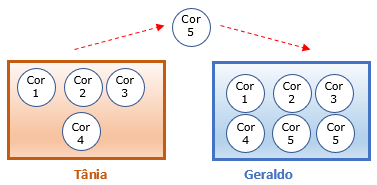
Geraldo escolherá ao acaso, de sua urna, uma bola para transferir para a urna de Tânia.
Ao final das transferências, as duas urnas voltarão às suas configurações iniciais se, e somente se, a bola escolhida por Geraldo for da mesma cor da que Tânia havia transferido para a sua urna.
Como são [tex]6[/tex] bolas, a probabilidade de que esse fato aconteça é [tex]\dfrac{2}{6}=\fcolorbox{black}{#eee0e5}{$\dfrac{1}{3}$} \, .[/tex]
(É importante observar que os dados relativos à urna da Tânia são necessários apenas para definir que uma segunda bola de uma determinada cor, seja ela qual for, foi transferida para a urna do Geraldo.)
Solução elaborada pelos Moderadores do Blog.
