✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Difícil)
Alguém utilizou a pia do banheiro de uma escola e não fechou adequadamente a torneira. Essa torneira ficou pingando das 18 horas até às 7 da manhã do dia seguinte, despejando na pia cerca de [tex]280[/tex] gotas de água por minuto.
Sabendo que [tex]20[/tex] gotas equivalem a [tex]1 \, ml[/tex] de água:
(a) determine quantos litros de água foram desperdiçados pela desatenção de quem deixou a torneira pingando.
(b) construa uma tabela que mostre, por hora, o total de água desperdiçada, em centímetros cúbicos.
(c) para não ter que construir uma tabela "enoooooooooorme", encontre uma equação que defina o total em centímetros cúbicos de água desperdiçada por minuto. Esboce o gráfico da função que essa equação define de [tex]\mathbb{R}[/tex] em [tex]\mathbb{R}[/tex].
Solução
Observe inicialmente que:
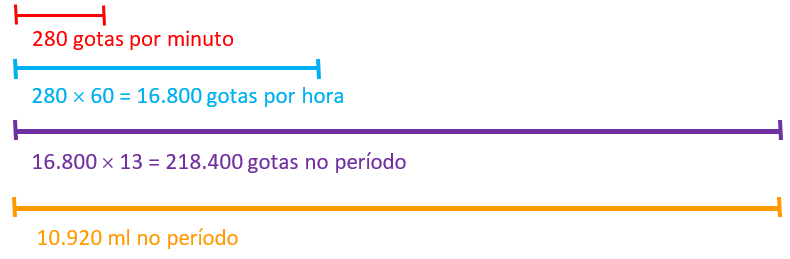
- A torneira da escola ficou pingando das [tex]18[/tex] horas até às [tex]7[/tex] da manhã do dia seguinte; portanto, por [tex]13[/tex] horas seguidas.
- Essa torneira despejou na pia cerca de [tex]280[/tex] gotas de água por minuto, ou seja, [tex]280\times 60=16 \, 800[/tex] gotas por hora, o que resultou em [tex]16 \, 800\times 13=218 \, 400[/tex] gotas no período de [tex]13[/tex] horas.
Como [tex]20[/tex] gotas equivalem a [tex]1 \, ml[/tex] de água, podemos utilizar uma regra de três simples para determinar o equivalente a [tex]218 \, 400[/tex] gotas em [tex]ml[/tex]:
| [tex]20[/tex] gotas | ————————————– | [tex]1 \, ml[/tex] |
| [tex]218 \, 400[/tex] gotas | ————————————– | [tex]x \, ml[/tex] |
Assim, resulta que
[tex]\qquad x=\dfrac{218 \, 400}{20}=10 \, 920,[/tex]
e, portanto, foram esperdiçados [tex]\boxed{10 \, 920 \, ml}[/tex] no período de [tex]13[/tex] horas em que a torneira ficou pingando.
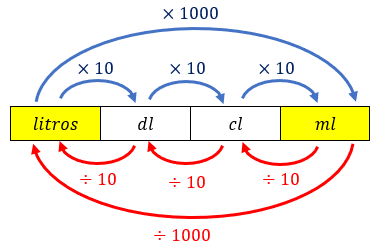
(a) Para determinar quantos litros de água foram esperdiçados pela desatenção de quem deixou a torneira pingando, vamos utilizar o esquema de conversão abaixo. Com ele, podemos perceber que [tex]1 \, l=1000 \, ml[/tex]; assim, [tex]10 \, 920 \, ml=10,92 \, l[/tex] e, portanto, foram esperdiçados aproximadamente [tex] \, \fcolorbox{black}{#eee0e5}{$ \, 11 \, litros$} \, [/tex] de água nas [tex]13[/tex] horas em que a torneira ficou pingando.
(b) Como [tex]\boxed{1 \, ml=1 \, cm^3} \, [/tex], vamos calcular a quantidade de água esperdiçada por hora, em [tex]ml[/tex], para construir a tabela.
Sabemos que a torneira despejou na pia cerca de [tex]16 \, 800[/tex] gotas por hora e que [tex]20[/tex] gotas equivalem a [tex]1 \, ml[/tex]; assim, vamos utilizar uma regra de três simples para determinar o equivalente a [tex]16 \, 800[/tex] gotas em [tex]ml[/tex]:
| [tex]20[/tex] gotas | ————————————– | [tex]1 \, ml[/tex] |
| [tex]16 \, 800[/tex] gotas | ————————————– | [tex]z \, ml[/tex] |
Logo, segue que [tex]z=\dfrac{16 \, 800}{20}=840,[/tex] ou seja, foram esperdiçados [tex]840 \, ml=\boxed{840 \, cm^3}[/tex] de água por hora.
Veja a tabela:
| Até às | Volume de água esperdiçado |
| 19 h | [tex]840 \, cm^3[/tex] |
| 20 h | [tex]1 \, 680 \, cm^3[/tex] |
| 21 h | [tex]2 \, 520 \, cm^3[/tex] |
| 22 h | [tex]3 \, 360 \, cm^3[/tex] |
| 23 h | [tex]4 \, 200 \, cm^3[/tex] |
| 24 h | [tex]5 \, 040 \, cm^3[/tex] |
| 1 h | [tex]5 \, 880 \, cm^3[/tex] |
| 2 h | [tex]6 \, 720 \, cm^3[/tex] |
| 3 h | [tex]7 \, 560 \, cm^3[/tex] |
| 4 h | [tex]8 \, 400 \, cm^3[/tex] |
| 5 h | [tex]9 \, 240 \, cm^3[/tex] |
| 6 h | [tex]10 \, 080 \, cm^3[/tex] |
| 7 h | [tex]10 \, 920 \, cm^3[/tex] |
(c) Como [tex]\boxed{1 \, ml=1 \, cm^3} \, [/tex] e [tex]20[/tex] gotas equivalem a [tex]1 \, ml[/tex], então [tex]20[/tex] gotas equivalem a [tex]1 \, cm^3.[/tex] A torneira despejou na pia cerca de [tex]280[/tex] gotas de água por minuto, ou seja, [tex]Q=\dfrac{280}{20}=14 \, cm^3[/tex] por minuto, conforme você pode comprovar com a regra de três indicada abaixo.
| [tex]20[/tex] gotas | ————————————– | [tex]1 \, cm^3[/tex] |
| [tex]280[/tex] gotas | ————————————– | [tex]Q \, cm^3[/tex] |
Dessa forma em [tex]\boxed{n}[/tex] minutos, a torneira despejou na pia [tex]\boxed{14n} \, cm^3[/tex] de água e a expressão [tex]Q(n)=14n[/tex] fornece, então, o total em centímetros cúbicos de água desperdiçada por [tex]n[/tex] minutos.
Podemos considerar a função definida como
[tex]\begin{align*}Q:& \, \mathbb{R} \rightarrow \mathbb{R}\\
&Q(x)=14x
\end{align*}\;[/tex]
cujo gráfico é o exibido abaixo.
Para uma melhor visualização, utilizamos uma proporção de [tex]10:200.[/tex]
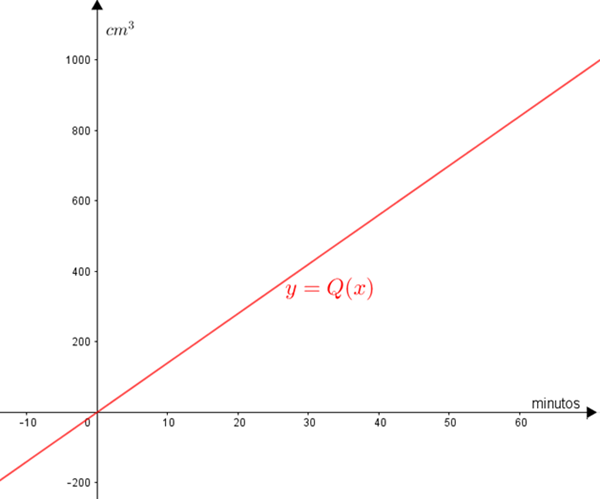
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
