Problema
(Indicado a partir do 8º ano do E. F.)
(Olimpíada de Matemática Espanhola, 2014 – Adaptado) Lila gosta muito de brincar com formas geométricas e números. Sabendo disso, seu pai lhe propôs dois desafios:
Distribuir os números [tex]0,1,2,3,4,5,6,7,8,9[/tex] sobre uma circunferência, de modo que a soma de quaisquer três números colocados sucessivamente seja,
- Desafio 1: no máximo, [tex]13.[/tex]
- Desafio 2: no máximo, [tex]15.[/tex]
Lila conseguirá cumprir os dois desafios?
Solução
Vamos supor que os dez números [tex]0,1,2,3,4,5,6,7,8,9[/tex] sejam distribuídos sobre uma circunferência conforme mostra a figura a seguir, na qual representamos os números não nulos pelas letras [tex]a,b,c,d,e,f,g,h,i.[/tex]
Feita a distribuição dos dez números, vamos cortar a circunferência na marca do [tex]0[/tex] e esticá-la.
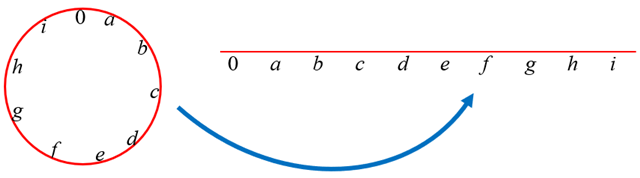
Independentemente da ordem em que foram distribuídos, perceba que
[tex]\quad a+b+c+d+e+f+g+h+i=1+2+3+4+5+6+7+8+9\\
\quad a+b+c+d+e+f+g+h+i=45, \quad \textcolor{#800000}{(i)}[/tex]
já que a adição é uma operação comutativa.
► Desafio 1
Se os números foram distribuídos de modo que a soma de quaisquer três números colocados sucessivamente seja, no máximo, [tex]13[/tex], particularmente podemos considerar os seguintes grupos de três números sucessivos:
- [tex]\boxed{a,b,c} \, , \, \boxed{d,e,f} \, , \, \boxed{g,h,i}[/tex].
Neste caso, temos as seguintes somas parciais:
- [tex]\boxed{a+b+c} \, , \, \boxed{d+e+f} \, , \, \boxed{g+h+i}[/tex]
todas, no máximo, iguais a [tex]13.[/tex]
Dessa forma,
[tex]\qquad \boxed{a+b+c \leqslant 13} \, ; \, \boxed{d+e+f\leqslant 13} \, ; \, \boxed{g+h+i \leqslant 13}[/tex],
e, então
[tex]\quad a+b+c+d+e+f+g+h+i=(a+b+c)+(d+e+f)+(g+h+i)\\
\quad a+b+c+d+e+f+g+h+i \leqslant 13+13+13=39.[/tex]
Com isso, temos
[tex]\qquad a+b+c+d+e+f+g+h+i \leqslant 39[/tex],
o que contraria a conclusão [tex]\textcolor{#800000}{(i)}.[/tex]
► Portanto, Lila NÃO conseguirá cumprir o Desafio 1.
► Desafio 2
Se os números foram distribuídos de modo que a soma de quaisquer três números colocados sucessivamente seja, no máximo, [tex]15[/tex], para os grupos genéricos
- [tex]\boxed{a,b,c} \, , \, \boxed{d,e,f} \, , \, \boxed{g,h,i}[/tex].
temos que
[tex]\qquad \boxed{a+b+c \leqslant 15} \, ; \, \boxed{d+e+f\leqslant 15} \, ; \, \boxed{g+h+i \leqslant 15}[/tex],
e, agora
[tex]\qquad a+b+c+d+e+f+g+h+i=(a+b+c)+(d+e+f)+(g+h+i)\\
\qquad a+b+c+d+e+f+g+h+i \leqslant 15+15+15=45\,,[/tex]
logo
[tex]\qquad a+b+c+d+e+f+g+h+i \leqslant 45.[/tex]
Mas isso não significa que exista tal distribuição, necessariamente; precisamos exibir efetivamente uma distribuição na qual a soma de quaisquer três números colocados sucessivamente na circunferência seja, no máximo, [tex]15.[/tex]
Seguem três sequências, que quando colocadas sobre uma circunferência satisfazem a condição requerida:
- ► [tex] \, 3 \, – \, 8 \, – \, 1 \, – \, 5 \, – \, 9 \, – \, 0 \, – \, 6 \, – \, 7 \, – \, 2 \, – \, 4[/tex];
► [tex] \, 0 \, – \, 9 \, – \, 5 \, – \, 1 \, – \, 8 \, – \, 4 \, – \, 3 \, – \, 2 \, – \, 7 \, – \, 6 [/tex];
► [tex] \, 7 \, – \, 2 \, – \, 4 \, – \, 9 \, – \, 0 \, – \, 6 \, – \, 8 \, – \, 1 \, – \, 5 \, – \, 3[/tex].
Vamos testar a primeira sequência, determinando todas as possíveis somas de grupos de três números colocados sucessivamente.
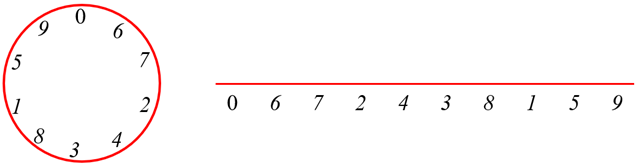
[tex]\qquad \boxed{3+8+1=12} \, , \, \boxed{5+9+0=14} \, , \, \boxed{6+7+2=15} \, , \, \boxed{4+3+8=15} \\
\qquad \boxed{1+5+9=15} \, , \, \boxed{0+6+7=13} \, , \, \boxed{2+4+3=9} \, \, \, , \, \boxed{8+1+5=14} \\
\qquad \boxed{9+0+6=15} \, , \, \boxed{7+2+4=13} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
