Problema
(Indicado a partir do 6º ano do E. F.)
Na adição de três números naturais representada abaixo, cada um com três algarismos, letras iguais correspondem a algarismos iguais.
\begin{equation}
+\begin{array}{r}
a\;b\;c \\
a\;b\;c \\
a\;b\;c \\
\hline
2\;c\;4\;4
\end{array}
\end{equation}
Calcule o valor do produto [tex]a\cdot b\cdot c[/tex].
Solução 1
Para a solução do problema vamos começar analisando os algarismos das unidades das três parcelas da adição.
- Notemos que a única possibilidade para [tex]c[/tex] é [tex]c=8[/tex], pois devemos ter [tex]3\cdot c[/tex] com unidade [tex]4[/tex]. Assim,
- Agora, para a soma [tex]3\cdot b+2[/tex] devemos obter um resultado cujo algarismo da unidade seja [tex]4[/tex]; logo, temos que [tex]b=4[/tex], então
- Por fim, para que [tex]3\cdot a+1[/tex] seja igual [tex]28[/tex] devemos ter [tex]a=9[/tex], ou seja,
\begin{equation}
+\begin{array}{r}
\;\;\;2\;\;\;\\
\;\;a\; b\;8 \\
\;\;a\;b\;8 \\
\;\;a\;b\;8 \\
\hline
2\;8\;4\;4
\end{array}
\end{equation}
\begin{equation}
+\begin{array}{r}
1\;2\;\;\;\\
\;\;a\; 4\;8 \\
\;\;a\;4\;8 \\
\;\;a\;4\;8 \\
\hline
2\;8\;4\;4
\end{array}
\end{equation}
\begin{equation}
+\begin{array}{r}
1\;2\;\;\;\\
\;\;9\; 4\;8 \\
\;\;9\;4\;8 \\
\;\;9\;4\;8 \\
\hline
2\;8\;4\;4
\end{array}
\end{equation}
Portanto, [tex] \, \fcolorbox{black}{#eee0e5}{$a\cdot b\cdot c=9\cdot 4\cdot 8=288$}[/tex].
Solução elaborada pelos Moderadores do Blog.
Solução 2
Para a solução do problema vamos começar analisando os algarismos das unidades das três parcelas da adição. Notemos que a única possibilidade para [tex]c[/tex] é [tex]c=8[/tex], pois devemos ter [tex]3⋅c[/tex] com unidade [tex]4[/tex]. Assim,
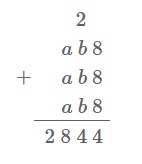
Como [tex]2844[/tex] é escrito como soma de três parcelas iguais a [tex]ab8[/tex], temos que [tex]2844=3\cdot (ab8)[/tex]. Logo, divindo [tex]2844[/tex] por [tex]3[/tex] obtemos [tex]948[/tex], ou seja, [tex]a=9[/tex] e [tex]b=4[/tex].
Com isso, [tex] \, \fcolorbox{black}{#eee0e5}{$a\cdot b\cdot c=9\cdot 4\cdot 8=288$}[/tex].
Solução elaborada pelos Moderadores do Blog.
