Problema
(Indicado a partir do 6º ano do E. F.)
Uma escola tem mil alunos e cada um deles possui um armário. Os armários estão enfileirados num corredor e numerados de [tex] 1[/tex] a [tex] 1000[/tex] . Indicando cada aluno pelo número de seu armário, o professor de Matemática da escola propôs a seguinte atividade:
(1) Os armários estão inicialmente todos fechados, mas destrancados.
(2) Ordenadamente, cada aluno [tex]n[/tex] passará pelos armários mudando a situação (abrindo o que está fechado, ou fechando o que está aberto) daqueles armários cujo número é divisível por [tex]n[/tex].
Quantos armários estarão abertos após o término da atividade?
Solução
Perceba que quando o aluno [tex]n[/tex] passar pelos armários ele só alterará a disposição dos armários cuja numeração é divisível por [tex]n[/tex]. Deste modo, após todos os alunos passarem pelos armários, ficarão abertos apenas os armários cuja numeração possuir um número ímpar de divisores.
Estes números, então, quando fatorados terão apenas potências de primos com expoente par (Veja o texto sobre divisores de um número natural que publicamos aqui.), sendo portanto os quadrados perfeitos menores do que [tex] 1000. [/tex]
Como [tex] 31^2 \lt 1000\,[/tex] e [tex]\,32^2 \gt 1000[/tex] , ficarão abertos [tex] 31[/tex] armários.
Solução elaborada pelos Moderadores do Blog.
Uma pequena simulação para ajudar
Para ajudar no entendimento do enunciado e da solução, apresentamos uma simulação do problema para dez alunos e, consequentemente, dez armários.
Na tabela abaixo, sinalizamos apenas as mudanças ocorridas durante as passagens de cada aluno pelos armários:
- com a letra A indicamos que uma porta fechada foi aberta,
- com a letra F indicamos que uma porta aberta foi fechada,
- as células em branco indicam as portas cujas situações não foram modificadas.
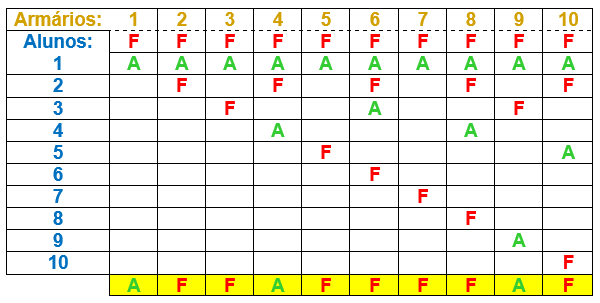
Observe na última linha da tabela a situação final de todas as portas após a passagem dos dez alunos.
A partir dos dados a seguir, perceba que os armários que ficaram abertos são aqueles que têm, de fato, um número ímpar de divisores.
- Divisores de [tex]1[/tex]: [tex]1[/tex] (um divisor).
- Divisores de [tex]2[/tex]: [tex]1[/tex] e [tex]2[/tex] (dois divisores).
- Divisores de [tex]3[/tex]: [tex]1[/tex] e [tex]3[/tex] (dois divisores).
- Divisores de [tex]4[/tex]: [tex]1[/tex], [tex]2[/tex] e [tex]4[/tex] (três divisores).
- Divisores de [tex]5[/tex]: [tex]1[/tex] e [tex]5[/tex] (dois divisores).
- Divisores de [tex]6[/tex]: [tex]1[/tex], [tex]2[/tex], [tex]3[/tex] e [tex]6[/tex] (quatro divisores).
- Divisores de [tex]7[/tex]: [tex]1[/tex] e [tex]7[/tex] (dois divisores).
- Divisores de [tex]8[/tex]: [tex]1[/tex], [tex]2[/tex], [tex]4[/tex] e [tex]8[/tex] (quatro divisores).
- Divisores de [tex]9[/tex]: [tex]1[/tex], [tex]3[/tex] e [tex]9[/tex] (três divisores).
- Divisores de [tex]10[/tex]: [tex]1[/tex], [tex]2[/tex], [tex]5[/tex] e [tex]10[/tex] (quatro divisores).
Note, também, que [tex]1[/tex], [tex]4[/tex] e [tex]9[/tex] são os quadrados perfeitos menores do que [tex]10[/tex] ([tex]1^2[/tex], [tex]2^2[/tex], [tex]3^2[/tex]).
