Problema
(Indicado a partir do 1º ano do E. M.)
(I Giochi di Archimede – Itália – 1996 – Adaptado) Qual é a soma dos números na tabela a seguir?
[tex]\begin{array}{|c|c|c|c|}
\hline
1 & 2 &3 & \cdots & n \\ \hline
2 & 3 &4 & \cdots & n+1 \\ \hline
3 & 4 &5 & \cdots & n+2 \\ \hline
\cdots & \cdots &\cdots & \cdots & \cdots \\ \hline
n& n+1 &n+2 & \cdots &2 n-1 \\ \hline
\end{array}[/tex]
Solução 1
Observe que a tabela do problema possui [tex]n[/tex] linhas e [tex]n[/tex] colunas; logo ela tem [tex]n^2[/tex] números.
Além disso, ao somarmos dois números que estão em posições simétricas com relação à diagonal da tabela (que é formada só de [tex]n[/tex]’s), obteremos sempre o valor [tex]2n[/tex].
Na tabela da figura a seguir, as células de tal diagonal estão destacadas em amarelo e alguns pares de números em posições simétricas estão destacados com a mesma cor (pares em azul, verde ou vermelho).
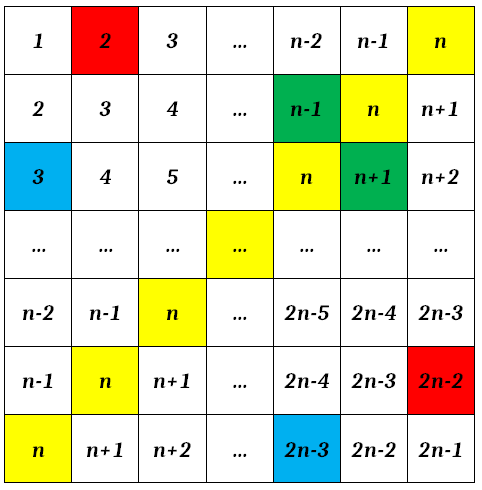
Assim, visando calcular a soma final, podemos construir uma nova tabela, na qual cada par de números simétricos poderia ser substituído por um par de [tex]n[/tex]’s. A soma dos números desta nova tabela seria igual à soma da tabela original.
Por exemplo, se trocarmos cada um dos números [tex]2[/tex] e [tex]2n-2[/tex] (em vermelho na figura anterior) por [tex]n[/tex] (em amarelo na figura a seguir), obtemos uma nova tabela na qual a soma de todos os números é igual a soma de todos os números da anterior. Isto porque [tex]2+ (2n-2)=n+n[/tex].
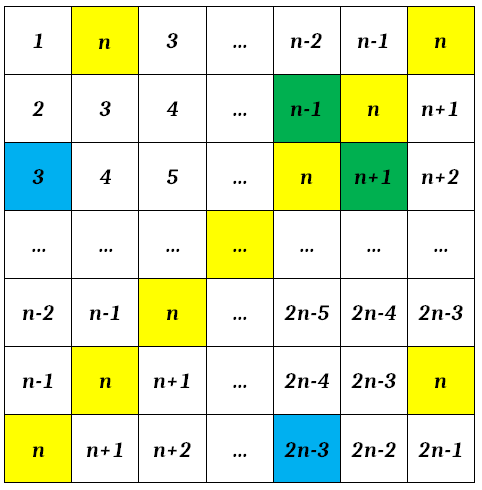
Podemos repetir o argumento anterior para os números [tex]3[/tex] e [tex]2n-3[/tex] (em azul na tabela da figura anterior), obtendo uma nova tabela (como a da figura a seguir) na qual a soma de todos os números é igual à soma dos números da tabela original.
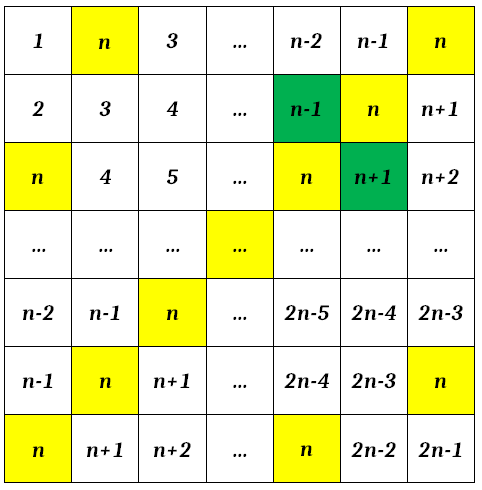
Seguindo esse argumento para cada par de números simétricos existentes na tabela original, obteremos ao final uma tabela composta somente de [tex]n[/tex]’s. Portanto, a soma original é igual à soma de [tex]n^2[/tex] números [tex]n[/tex], ou seja, [tex]n^3[/tex].
Solução elaborada pelos Moderadores do Blog.

Ajuda para a Solução 2
A soma dos [tex]t[/tex] primeiros números naturais não nulos é dada por
[tex]\qquad \qquad \boxed{1+2+3+ \cdots+t=\dfrac{(1+t)\cdot t}{2}}[/tex]. (Se precisar, visite esta página.)
De modo geral, a soma dos [tex]t \, [/tex] primeiros termos de uma progressão aritmética
[tex]\qquad \qquad\left(x_1 \, , \, x_2 \, , \, x_3 \, , \, \cdots \, , \, x_t \, , \, \cdots \right)[/tex]
é dada por:
[tex]\qquad \qquad\boxed{\dfrac{\left(x_1+x_t \right)\cdot t}{2}}[/tex].
Solução 2
Podemos resolver este problema utilizando as fórmulas da Ajuda para somarmos, inicialmente, os números das linhas (ou colunas):
- [tex]1+2+3+\cdots+n=\boxed{\dfrac{(n+1)\cdot n}{2}}[/tex]
- [tex]2+3+4+\cdots+(n+1)=\boxed{\dfrac{(n+3)\cdot n}{2}}[/tex]
- [tex]3+4+5+\cdots+(n+2)=\boxed{\dfrac{(n+5)\cdot n}{2}}\\
\qquad \qquad \vdots[/tex] - [tex]n+(n+1)+(n+2)+\cdots+\underbrace{(n+(n-1))}_{2n-1}=\boxed{\dfrac{(n+(2n-1))\cdot n}{2}}[/tex].
Somando agora essas [tex]n[/tex] somas parciais, obtemos a soma final [tex]S[/tex]:
[tex] \, \, \,\\
\qquad \begin{align*} S &= \dfrac{(n+1)\cdot n}{2}+\dfrac{(n+3)\cdot n}{2}+\dfrac{(n+5)\cdot n}{2}+\cdots +\dfrac{(n+(2n-1))\cdot n}{2}\\
&= \dfrac{n}{2}\cdot \left[(n+1)+(n+3)+(n+5)+ \cdots +(n+(2n-1))\right]\\
&= \dfrac{n}{2}\cdot \left[(n+n+\cdots+n)+(1+3+5+\cdots +(2n-1))\right]\\
&= \dfrac{n}{2}\cdot \left[n^2+\dfrac{(1+(2n-1))\cdot n}{2}\right]\\
&= \dfrac{n}{2}\cdot \left[n^2+\dfrac{\cancel{2}n\cdot n}{\cancel{2}}\right]\\
&= \dfrac{n}{2}\cdot (2n^2)\\
&=n^3.\end{align*}[/tex]
Portanto, a soma de todos os números da tabela do problema é [tex] \, \fcolorbox{black}{#eee0e5}{$ \, n^3$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
