Problema
(Indicado a partir do 9º ano do E. F.)
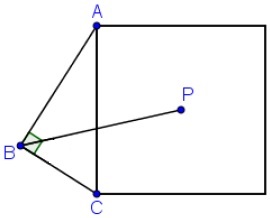
Na figura, seja [tex]P[/tex] o centro do quadrado construído sobre a hipotenusa [tex]AC[/tex] do triângulo retângulo [tex]ABC[/tex]. Calcule a medida do ângulo [tex]P\hat B C[/tex].

Lembretes
[tex]\textcolor{#800000}{(1)}[/tex] A diagonal de um quadrado é também bissetriz.
[tex]\textcolor{#800000}{(2)}[/tex] A soma das medidas dos ângulos internos de um triângulo é [tex]180^{\circ}[/tex].
[tex]\textcolor{#800000}{(3)}[/tex] Se a soma dos ângulos opostos de um quadrilátero for [tex]180^{\circ}[/tex], então este quadrilátero é inscritível numa circunferência.
[tex]\textcolor{#800000}{(4)}[/tex] Se dois ângulos inscritos enxergam o mesmo arco de circunferência, então eles são congruentes. (Para aprender mais sobre ângulos centrais e inscritos, dê uma passadinha por esta Sala de Estudos.)
Solução
Leia com atenção as explicações de como obter as medidas que aparecem na figura abaixo.
- Como [tex]P[/tex] é o centro do quadrado, os segmentos [tex]\overline {AP}[/tex] e [tex]\overline {CP}[/tex] fazem parte de suas diagonais. Pelo Lembrete [tex]\textcolor{#800000}{(1)}[/tex], os ângulos [tex]P\hat A C[/tex] e [tex]P\hat C A[/tex] medem [tex]45^\circ[/tex]. Pelo Lembrete [tex]\textcolor{#800000}{(2)}[/tex], o ângulo [tex]A\hat P C[/tex] vale [tex]90^\circ[/tex].
Perceba que o quadrilátero [tex]PABC[/tex] possui ângulos opostos com soma [tex]180^\circ[/tex]. Pelo Lembrete [tex]\textcolor{#800000}{(3)}[/tex], este quadrilátero é inscritível numa circunferência.
Chamemos de [tex]x[/tex] a medida do ângulo [tex]P\hat B C[/tex].
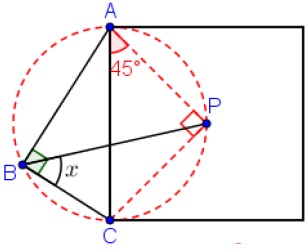
Note que, na circunferência mostrada na figura acima, os ângulos inscritos [tex]P\hat B C[/tex] e [tex]P\hat A C[/tex] enxergam o mesmo arco [tex]\stackrel{\frown}{PC}[/tex]. Logo, pelo Lembrete [tex]\textcolor{#800000}{(4)}[/tex], esses ângulos são congruentes.
Portanto, [tex]\fcolorbox{black}{#eee0e5}{$x=45^\circ$}[/tex] .
Solução elaborada pelos Moderadores do Blog.
