Problema
(Indicado a partir do 1º ano do E. M.)
Em uma escola existem [tex]900[/tex] alunos. Para organizar uma gincana esportiva, foi observado que:
- [tex]330[/tex] alunos praticam voleibol;
- [tex]360[/tex] alunos praticam futebol;
- [tex]220[/tex] alunos praticam basquetebol;
- [tex]200[/tex] alunos praticam handebol.
Para cada dupla de modalidades, o número de alunos que praticam exatamente as duas modalidades esportivas é [tex]20[/tex]. Para cada trio de modalidades, existem [tex]30[/tex] alunos que praticam exatamente as três modalidades, e existem [tex]40[/tex] alunos que praticam as quatro modalidades. Com base nas informações apresentadas, calcule:
(a) o número de alunos que praticam somente uma modalidade.
(b) o número de alunos que praticam exatamente duas modalidades.
(c) o número de alunos que não praticam nenhuma das modalidades.
Ajuda
Diagramas de Venn são representações esquemáticas que permitem visualizarmos conjuntos como se fossem regiões do plano. A partir de um conjunto universo, os vários conjuntos envolvidos são limitados por figuras fechadas, como círculos, quadrados, retângulos e losangos. O interior de cada figura representa os elementos do respectivo conjunto. Tente representar o problema em um Diagrama de Venn com quatro conjuntos, além do universo. Lembre-se de que todas as interseções e uniões possíveis devem ser representadas por alguma região do esquema.
 |
Diagramas de Venn para mais de três conjuntos, além do universo, não são triviais. Para aprender mais sobre o tema, dê uma passadinha nesta Sala do nosso Blog. |
Solução
Para ajudar na solução do problema, vamos utilizar um Diagrama, como o desta figura.
Vamos preencher a quantidade de alunos no diagrama de acordo com as informações do problema.
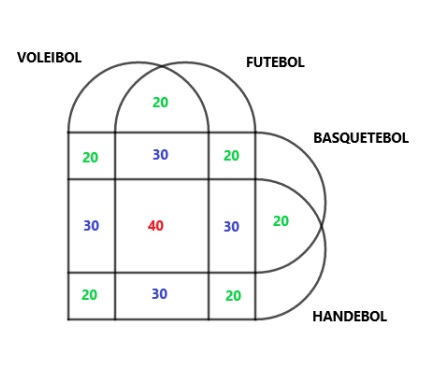
- Como existem [tex]\textcolor{red}{40}[/tex] alunos que praticam as quatro modalidades, essa quantidade deve aparecer na interseção dos quatro conjuntos.
- Também existem [tex]\textcolor{blue}{30}[/tex] alunos que praticam exatamente três modalidades, para cada trio de modalidades. Assim, devemos localizar no diagrama os espaços compreendidos pela interseção de exatamente três conjuntos.
- E, finalmente, como existem [tex]\textcolor{#00EE00}{20}[/tex] alunos que praticam exatamente duas modalidades esportivas para cada dupla de modalidades, devemos procurar no diagrama os lugares correspondentes à interseção de somente dois conjuntos. Logo, obtemos a seguinte disposição no diagrama.
- Agora, temos que [tex]330[/tex] alunos praticam voleibol, mas no conjunto que representa essa modalidade já temos um total de [tex]190[/tex] alunos. Logo, o número de alunos que só praticam voleibol é [tex]140[/tex]. Seguindo o mesmo raciocínio, obtemos que [tex]170[/tex] alunos praticam somente futebol, [tex]30[/tex] somente basquetebol e [tex]10[/tex] somente handebol.
Portanto, completamos o nosso diagrama, conforme mostra a figura abaixo. Observem que não representamos o conjunto universo no diagrama, pois ele não contribui para a solução do problema.
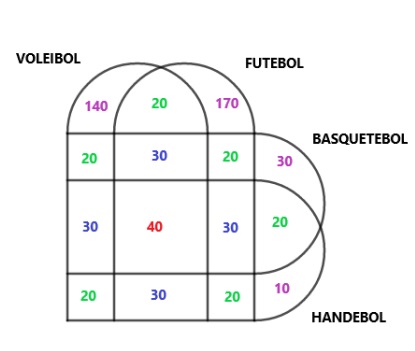
Finalmente, podemos responder as questões do problema!
(a) O número de alunos que praticam somente uma modalidade é [tex]140+170+30+10=\fcolorbox{black}{#eee0e5}{$350$} \, .[/tex]
(b) O número de alunos que praticam exatamente duas modalidades é [tex]20+20+20+20+20+20=\fcolorbox{black}{#eee0e5}{$120$} \, .[/tex]
(c) Temos um total de [tex] 900[/tex] alunos na escola; vamos subtrair desse número o total de alunos do diagrama. Vemos pela última figura, que o total de alunos que praticam as modalidades é [tex]630[/tex]. Portanto, temos [tex]900-630=\fcolorbox{black}{#eee0e5}{$270$}[/tex] alunos que não praticam nenhuma dessas modalidades.
Solução elaborada pelos Moderadores do Blog.
