Problema
(Indicado a partir do 2º ano do E. M.)
Marque seis pontos em um plano, como os ilustrados na figura abaixo, e tome dois lápis de cor, azul e vermelho, por exemplo. Conecte cada par de pontos com um segmento de uma das duas cores escolhidas inicialmente.
Conectados todos os segmentos, pergunta-se:
a) Quantos triângulos existirão ao final?
b) É possível executar a tarefa de modo que não haja qualquer triângulo com os três lados de uma mesma cor? Explique.
Solução
a) Para cada triângulo necessitamos de 3 vértices distintos.
– Para a escolha do primeiro vértice, temos 6 possibilidades.
– Para a escolha do segundo e terceiro, temos 5 e 4 possibilidades, respectivamente.
Isso resulta em [tex]6\times\ 5 \times\ 4=120[/tex] possibilidades.
Como a ordem da escolha dos vértices não altera o triângulo, (os triângulos ABC, ACB, BCA, BAC, CAB e CBA são todos os mesmos, por exemplo) para cada 3 vértices escolhidos, temos 6 composições iguais, o que nos leva a dividir o resultado obtido anteriormente por 6, ou seja, há um total de 20 triângulos possíveis.
b)Tentemos executar a tarefa evitando triângulos de uma mesma cor.
Para um dos pontos, digamos A, haverá 5 pontos a serem conectados.
Como dispomos de apenas duas cores, pelo PCP – Princípio das Casas dos Pombos – três desses segmentos, pelo menos, devem ser da mesma cor, digamos azul. Agora supomos que as extremidades desses segmentos sejam os pontos B, C e D. Se tivéssemos BC azul, então teríamos o triângulo ABC azul, o que não desejamos. Assim BC deve ser vermelho. Pelo mesmo argumento, se BD fosse azul, então teríamos o triângulo ABD azul, o que também não queremos. Logo, BD deve ser vermelho.
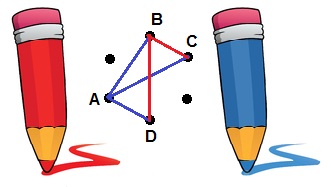
E agora? O que resta para CD? Se for azul, teremos o triângulo ACD azul. Por outro lado, se for vermelho, teremos o triângulo BCD vermelho…
Com isso, vemos que é impossível executar a tarefa proposta.
Solução elaborada pelos Moderadores do Blog.
