Problema
(Indicado a partir do 6º ano do E. F.)
[tex]27[/tex] pedaços de queijo com formato cúbico foram organizados de modo a formar um cubo maior, conforme mostra a figura abaixo.
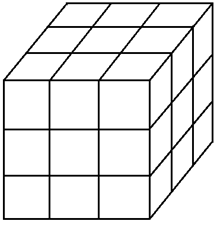
Um ratinho viu o queijo e quer comê-lo por inteiro…
Ele come um cubinho inteiro por dia e no dia seguinte ele come um cubinho vizinho.
(Entendamos por vizinhos dois pedaços com faces comuns.)
É possível que o ratinho coma o pedaço que está no centro no [tex]27^\circ[/tex] dia?
Solução
Não é possível, vejamos.
Pintando o cubo maior como mostra a figura abaixo, podemos concluir que o pedaço que fica no meio é branco. Deste modo, há [tex]14[/tex] pedaços pretos e [tex]13[/tex] pedaços brancos.

Observe que:
- Se o rato começa comendo um cubinho preto, no dia seguinte terá de comer um cubinho branco. No próximo dia ele come um preto, no dia seguinte come um branco, e assim sucessivamente. Dessa forma, na melhor das hipóteses, ele comeria o último pedaço branco no [tex]26^\circ[/tex]dia e sobraria um preto para o [tex]27^\circ[/tex]dia.
[tex]\qquad \qquad \underbrace{p \rightarrow b \rightarrow p \rightarrow b \rightarrow \cdots \rightarrow p \rightarrow b }_{26 \, cubinhos} \rightarrow \textcolor{red}{p}[/tex] - Já, se o rato começa comendo um cubinho branco, no [tex]25^\circ[/tex]dia ele comerá o último cubinho branco. Sobrariam, então, dois pedaços pretos (não vizinhos) para os [tex]26^\circ[/tex] e [tex]27^\circ[/tex]dias.
[tex]\qquad \qquad \underbrace{b \rightarrow p \rightarrow b \rightarrow p \rightarrow \cdots \rightarrow b }_{25 \, cubinhos} \rightarrow p \rightarrow \textcolor{red}{p}[/tex]
De qualquer forma, o ratinho comerá o último pedaço branco no [tex]25^\circ[/tex] dia ou no [tex]26^\circ[/tex] dia.
Sabemos que o pedaço que fica no meio é branco; assim, o ratinho não conseguirá comer o pedaço que está no centro no [tex]27^\circ[/tex] dia.
Solução elaborada pelos Moderadores do Blog.
Um applet para ajudar
Você pode utilizar o aplicativo abaixo para visualizar em 3D o cubo formado pelos [tex]27[/tex] cubinhos que colorimos de branco e preto para facilitar a solução do problema.
Além de rodar o cubo grande, você pode apagar os cubinhos que o compõem. Assim, você pode verificar que, de fato, o cubinho central é branco e até simular os dois casos explicitados na solução do problema.
Instruções:
(1) Espere o applet carregar completamente. (Ele pode demorar um pouquinho para carregar.)
(2) Para movimentar o cubo, clique em qualquer ponto da janela do aplicativo, mantenha o mouse pressionado e faça o movimento. (Se você estiver utilizando um celular ou um tablet, basta tocar levemente na janela do aplicativo e fazer o movimento.)
(3) Para deletar um cubinho colorido, clique nele com o botão esquerdo do mouse e delete-o. (Se você estiver utilizando um celular ou um tablet, pressione qualquer face do cubinho até que apareça uma janelinha com algumas opções. Nessa janelinha, clique na opção Apagar.)
(4) Se quiser voltar para a configuração inicial, clique nas setinhas circulares que aparecem no canto superior direito do aplicativo.
OBMEP_ srdg, criado com o GeoGebra
Observamos que o applet ajuda na visualização de resultados;
mas, matematicamente, não substitui suas explicações.
