Problema
(Indicado a partir do 2º ano do E. M.)
Gamão é um jogo de tabuleiro para dois jogadores, realizado num caminho unidimensional, no qual os adversários movem suas peças em sentidos contrários à medida que jogam dados e estes determinam quantas “casas” serão avançadas. Vencerá a partida o jogador que conseguir retirar primeiro todas as suas peças do tabuleiro.

Segundo as regras adotadas, o número total de casas que as peças de um jogador podem avançar numa dada jogada é determinado pelo resultado do lançamento de dois dados. Esse número é igual à soma dos valores obtidos nos dois dados, se esses valores forem diferentes entre si, e é igual ao dobro da soma, se os valores obtidos nos dois dados forem iguais. Supondo que os dados não sejam viciados, qual a probabilidade de um jogador poder fazer suas peças andarem pelo menos oito casas em uma jogada?
Solução
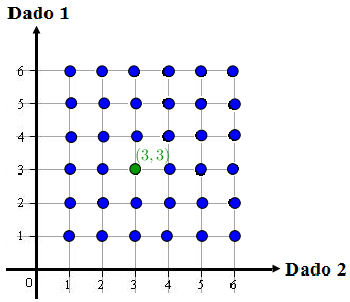
A figura mostra todas as [tex]6 \times 6=36[/tex] possibilidades que podem ocorrer quando do lançamento dos dois dados.
Observe que o ponto destacado, e denotado por [tex] \textcolor{green}{(3,3)}[/tex], representa o caso no qual os dois dados resultam em [tex]3[/tex] após seu lançamento.
Para que um jogador possa fazer suas peças andarem pelo menos oito casas em uma jogada, de acordo com as regras descritas no texto-base, todas as possibilidades favoráveis estão mostradas em destaque na próxima figura. Cada ponto representa
- um caso cuja soma dos resultados, após o lançamento dos dados, é no mínimo [tex]8[/tex];
- ou um caso no qual os resultados são iguais e o dobro de sua soma é no mínimo [tex]8[/tex].
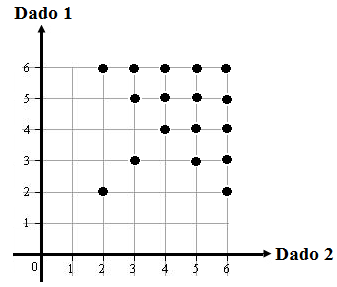
Deste modo, como são [tex]17[/tex] casos favoráveis dentre os [tex]36[/tex] possíveis, a probabilidade pedida é [tex] \, \fcolorbox{black}{#eee0e5}{$\dfrac{17}{36}$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
