Problema
(Indicado a partir do 8º ano do E. F.)
Aline desenha uma sequência de figuras, conforme a ilustração a seguir. Cada figura tem um quadrado a mais do que a figura anterior e esse quadrado que foi acrescentado tem lado igual à diagonal do maior quadrado da figura anterior. Além disso, todos os quadrados de cada figura têm um vértice comum. O quadrado da figura 1 tem área de [tex]4\ cm^2[/tex].
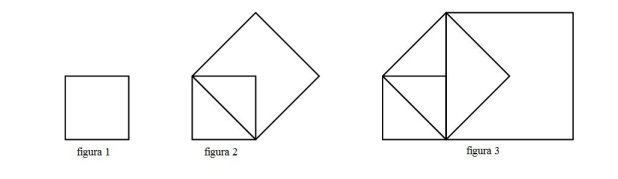
Determine a área total da figura 3.
Solução
Analisando a figura 3, observamos que a sua área total é [tex]\boxed{\frac{1}{2}A_{\textrm{quadrado 1}}+\frac{1}{2}A_{\textrm{quadrado 2}}+A_{\textrm{quadrado 3}}}.[/tex] Como conhecemos a área do quadrado da figura 1, precisamos calcular as áreas dos quadrados acrescentados nas figuras 2 e 3.
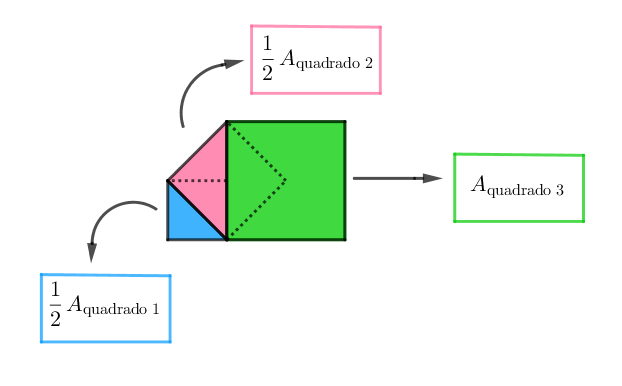
- Observe a figura 2. Para determinarmos a área do segundo quadrado construído, devemos observar que [tex]\frac{1}{4}[/tex] de sua área corresponde a [tex]\frac{1}{2}[/tex] da área do quadrado da figura 1. Dessa forma, temos:
- Analogamente, podemos utilizar o mesmo argumento para determinarmos a área do terceiro quadrado construído:
[tex]\begin{align}
A_{\textrm{quadrado 2}}&=4\times\frac{1}{2}A_{\textrm{quadrado 1}}\\
&=2\times A_{\textrm{quadrado 1}}\\
&=8\ cm^2\\
\end{align}
[/tex]
[tex]\begin{align}
A_{\textrm{quadrado 3}}&=4\times\frac{1}{2}A_{\textrm{quadrado 2}}\\
&=2\times A_{\textrm{quadrado 2}}\\
&=16\ cm^2\\
\end{align}
[/tex]
Assim, a área total da figura 3 é dada por:
[tex]\qquad \begin{align}
A_{\textrm{figura 3}}&=\frac{1}{2}A_{\textrm{quadrado 1}}+\frac{1}{2}A_{\textrm{quadrado 2}}+A_{\textrm{quadrado 3}}\\
&=\frac{1}{2}\times 4+\frac{1}{2}\times 8+16\\
&=2+4+16\\
&=\fcolorbox{black}{#eee0e5}{$22\ cm^2$} \, .
\end{align}
[/tex]
Solução elaborada pelos Moderadores do Blog.
