Problema
(Indicado a partir do 6º ano do E. F.)
O objetivo deste problema é distribuir os números naturais de 1 a 8 nos círculos indicados na figura, de maneira tal que não haja nenhum par de números consecutivos unidos por um segmento.
Isso é possível?
Justifique sua resposta, apresentando um argumento no caso de não ser possível ou indicando a estratégia utilizada em caso de preenchimento.
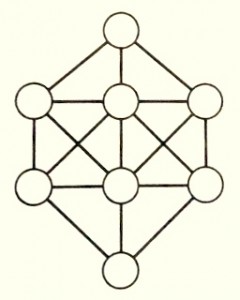
Solução
Uma solução possível é:
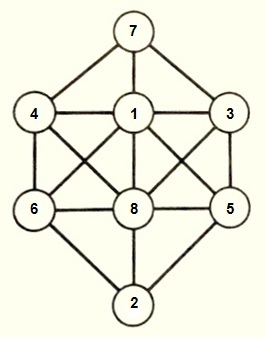 Justificativas do preenchimento:
Justificativas do preenchimento:
Observe, inicialmente, que as posições centrais podem apenas ser ocupadas pelos números 1 e 8, já que qualquer outro candidato teria dois números consecutivos a ele (antecessor e sucessor) e, sendo 6 as conexões a serem feitas (entre sete números que restariam por preencher), um dos consecutivos estaria, invariavelmente, ligado ao número. Sendo assim, automaticamente, temos o 7 e o 2 para as extremidades (contrárias às adjacentes de 8 e 1, respectivamente).
Continuemos o preenchimento pelo 6: ele deve estar na linha do 8; pois, caso contrário, seria adjacente ao 7. O lado, tanto faz; afinal temos uma situação simétrica.
Posto o 6, note que junto a ele só poderá ser o 4, pois se fosse o 3, teríamos o 4 e o 5 juntos no lado oposto (de modo análogo, se fosse o 5, teríamos o 3 e o 4 juntos no lado oposto), o que não pode acontecer.
Para o preenchimento do 3 e do 5, basta observar que o 3 não pode ser adjacente ao 2 e, assim, o diagrama estará completo.
Você conseguiria, agora, indicar outra possível solução?
Solução elaborada pelos Moderadores do Blog.
Participou da discussão do problema o Clube Math Error.
