Problema
(Indicado a partir do 6º ano do E. F.)
Ruth possui muitas caixas de dimensões [tex]5[/tex] cm[tex]\times 5[/tex] cm[tex]\times 5[/tex] cm. Certo dia resolveu empilhar todas as caixas e obteve a arrumação mostrada na figura a seguir.
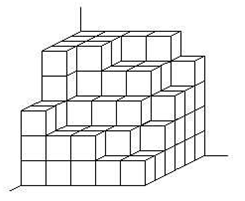
(a) Quantas caixas Ruth possui?
(b) Para completar um paralelepípedo com a base já mostrada e sem mexer nas caixas já existentes, quantas caixas a mais, no mínimo, Ruth precisaria ter?
Solução
(a) A quantidade de caixas por cada andar da pilha é
- [tex]1^\circ andar: 5\times 6=30[/tex]
- [tex]2^\circ andar: 5\times 6-3=27[/tex]
- [tex]3^\circ andar: 5\times 6-9=21[/tex]
- [tex]4^\circ andar: 14[/tex]
- [tex]5^\circ andar: 9.[/tex]
Assim, o total de caixas é a soma de todos esses valores, ou seja, [tex]\fcolorbox{black}{#eee0e5}{$101 \text{ caixas}$}\,.[/tex]
(b) O menor paralelepípedo completo que pode ser obtido a partir da figura terá dimensões [tex]6\times 5 \times 5[/tex]. Deste modo, seriam necessárias, no mínimo, mais [tex]6\times 5 \times 5-101=\fcolorbox{black}{#eee0e5}{$49\text{ caixas}$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
