✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Médio)
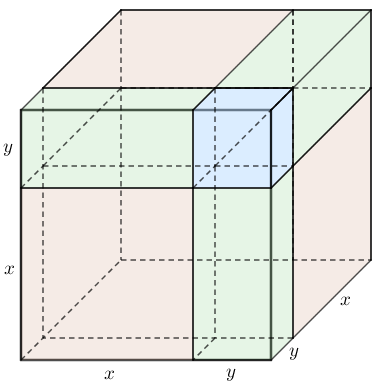
(Construindo Conhecimentos em Matemática (Bianchini/Miani) – Adaptado) Se [tex]x[/tex] e [tex]y[/tex] são números reais positivos, que produto notável pode ser interpretado geometricamente pela figura abaixo?
Solução
Observe atentamente que a nossa figura é um cubo cujas arestas têm comprimento [tex]x+y[/tex] e que foi dividido em dois cubos menores e em seis paralelepípedos, conforme ilustra a figura a seguir.
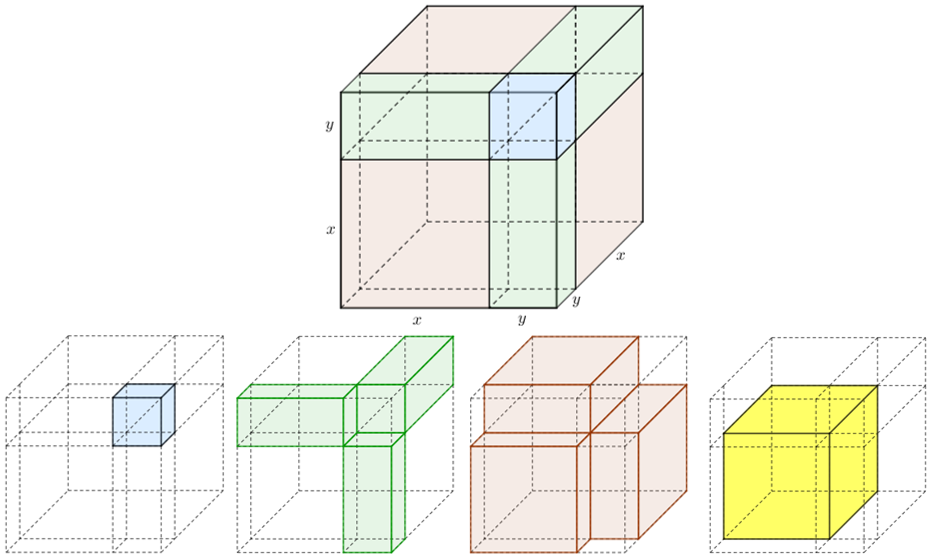
- Dessa forma, o volume do cubo maior é a soma dos volumes dos dois cubos menores e dos seis paralelepípedos.
Vamos calcular esses volumes separadamente; veja no applet abaixo as medidas das respectivas arestas de cada sólido.
Um applet para ajudar. . .
Para utilizar o applet:
(1) Espere o aplicativo carregar completamente.
(2) Clique no ícone ► que aparecerá no canto inferior esquerdo do aplicativo.
(3) Para parar a animação, clique no ícone || que aparece no canto inferior esquerdo do aplicativo em movimento.
(4) Para continuar com a animação do ponto onde você parou, clique no ícone ► que reapareceu no canto inferior esquerdo do aplicativo.
(5) Para retornar à posição inicial, clique nas setinhas circulares que aparecem no canto superior direito do aplicativo.
OBMEP_ srdg, criado com o GeoGebra
- O volume [tex]V[/tex] do cubo grande é [tex]\boxed{V=\left(x+y\right)^3} \, .[/tex]
- O volume [tex]V_1[/tex] do cubo colorido de amarelo e cujas arestas têm comprimento [tex]x[/tex] é [tex]\boxed{V_1=x^3} \, .[/tex]
- O volume [tex]V_2[/tex] de cada paralelepípedo colorido de verde e cujas arestas têm comprimentos [tex]x, \, y, \, y[/tex] é [tex]\boxed{V_2=xy^2} \, .[/tex]
- O volume [tex]V_3[/tex] de cada paralelepípedo colorido de marrom e cujas arestas têm comprimentos [tex]x, \, x, \, y[/tex] é [tex]\boxed{V_3=x^2y} \, .[/tex]
- O volume [tex]V_4[/tex] do cubo colorido de azul e cujas arestas têm comprimento [tex]y[/tex] é [tex]\boxed{V_4=y^3} \, .[/tex]
Mas sabemos que [tex]V=V_1+3V_2+3V_3+V_4[/tex], assim, a interpretação geométrica da figura em questão ilustra uma importante identidade algébrica que compõe a lista dos produtos notáveis:
[tex] \, \fcolorbox{black}{#eee0e5}{$\left(x+y\right)^3=x^3 +3xy^2+3x^2y+y^3$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
