Problema
(Indicado a partir do 8º ano do E. F.)
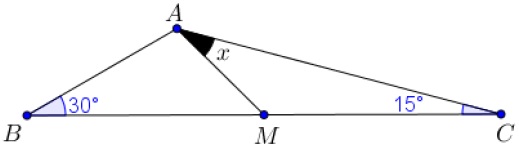
Determine o valor do ângulo [tex]x[/tex], sabendo que [tex]M[/tex] é ponto médio do segmento [tex]BC[/tex].

Lembretes e notação
(1) Se um triângulo inscrito à uma circunferência possui um dos lados como diâmetro, então esse triângulo é retângulo.
(2) A mediana de um triângulo retângulo com extremidade no vértice do ângulo reto mede a metade da hipotenusa.
(3) Todo triângulo isósceles possui os lados adjacentes à base congruentes e ângulos da base com mesma medida.
(4) Se um triângulo isósceles possui um ângulo interno medindo [tex]60^\circ[/tex], então esse triângulo é equilátero.
(5) A soma das medidas dos ângulos internos de um triângulo é [tex]180^\circ[/tex].
(6) Notação: Denotaremos o segmento definido por dois pontos, digamos [tex]A[/tex] e [tex]B[/tex], por [tex]AB[/tex] e o seu comprimento por [tex]\overline{AB}[/tex].
Solução
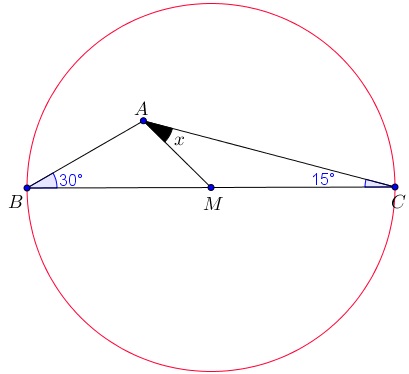
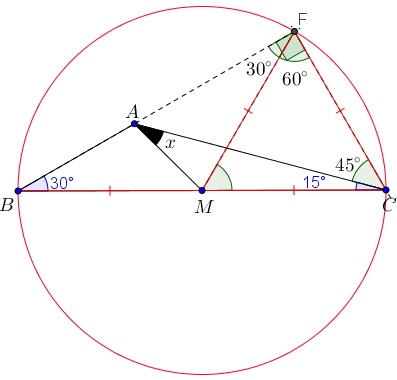
- Como [tex]M[/tex] é ponto médio do segmento [tex]BC[/tex], construindo a circunferência de centro [tex]M[/tex] e raio de comprimento [tex] \overline{MC}[/tex], podemos garantir que o ponto [tex]B[/tex] também pertence a essa circunferência.
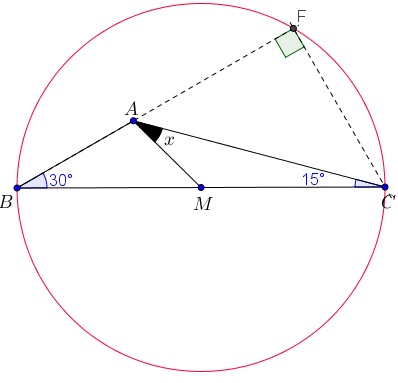
- Podemos, então, prolongar o segmento [tex]AB[/tex], interceptando a circunferência em um ponto [tex]F[/tex]. Pelo Lembrete 1, o triângulo [tex]BFC[/tex] é retângulo em [tex]F[/tex].
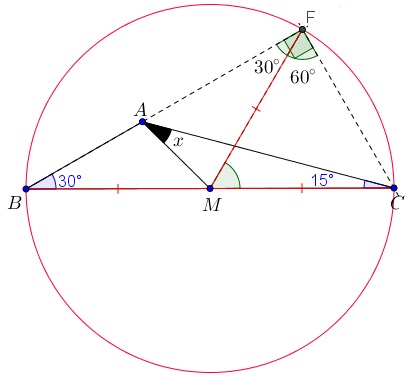
- De acordo com o Lembrete 2, a mediana [tex]FM[/tex] do triângulo [tex]BCF[/tex] é congruente aos segmentos [tex]MB[/tex] e [tex]MC[/tex]. Com isso, podemos construir dois triângulos isósceles [tex]FMB[/tex] e [tex]FMC[/tex]. Pelo Lembrete 3, obtemos que a medida do ângulo [tex]B\hat{F}M[/tex] é [tex]30^\circ[/tex] e, consequentemente, a medida do ângulo [tex]M\hat{F}C[/tex] é [tex]90^\circ-30^\circ=60^\circ[/tex].
- Agora, pelo fato de o triângulo [tex]FMC[/tex] ser isósceles e possuir um ângulo medindo [tex]60^\circ[/tex], pelo Lembrete 4, garantimos que ele é um triângulo equilátero. Portanto, o segmento [tex]FC[/tex] é congruente aos segmentos [tex]FM[/tex] e [tex]CM[/tex] e o ângulo [tex]F\hat{C}A[/tex] tem medida [tex]60^\circ-15^\circ=45^\circ.[/tex]
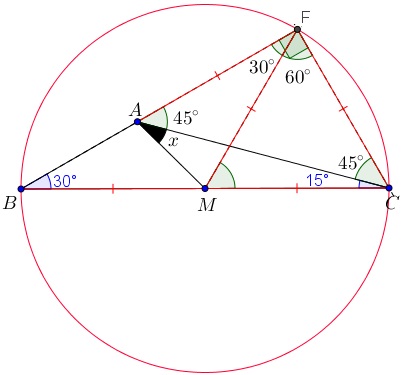
- Vamos analisar agora o triângulo [tex]FAC[/tex]. Pelo Lembrete 5, concluímos que o ângulo [tex]F\hat{A}C[/tex] mede [tex]180^\circ-90^\circ-45=45^\circ[/tex]. Portanto, o triângulo é isósceles, com [tex]FA[/tex] congruente a [tex]FC[/tex].
- Para finalizar, note que o triângulo [tex]FAM[/tex] também é isósceles. Novamente, pelo Lembrete 3, concluímos que o ângulo [tex]F\hat{A}M[/tex] possui a mesma medida que o ângulo [tex]F\hat{M}A[/tex].
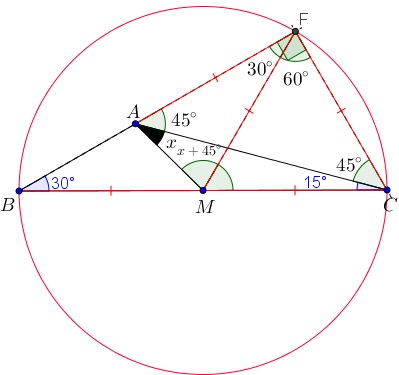
Finalmente, utilizando o Lembrete 5 no triângulo [tex]FAM[/tex], temos que [tex]\boxed{\left(x+45^\circ\right)+\left(x+45^\circ\right) +30^\circ=180^\circ}[/tex], donde concluímos que [tex] \, \fcolorbox{black}{#eee0e5}{$ x=30^\circ$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
