Problema
(Indicado a partir do 8º ano do E. F.)
Observe na imagem abaixo o padrão de uma construção de triângulos com palitos.
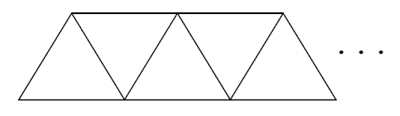
Mantendo o padrão da construção, responda:
a) Quantos palitos são necessários para formar [tex]2018[/tex] triângulos?
b) Com [tex]289[/tex] palitos, quantos triângulos serão construídos?
Solução
Note que no primeiro triângulo utilizamos três palitos. A partir deste, para construirmos cada novo triângulo, precisamos de mais dois palitos. Na tabela abaixo constam os dados da sequência mostrada na figura acima:
\begin{array}{|c|c|}
\hline
\textrm{Quantidade de Triângulos}&\textrm{Número de Palitos}\\\hline
1&3\\\hline
2&5\\\hline
3&7\\\hline
4&9\\\hline
5&11\\\hline
\vdots&\vdots\\\hline
\end{array}
Observe que na construção do primeiro triângulo utilizamos três palitos e na construção dos demais dois palitos, uma vez que um dos lados já está definido.
Assim, se [tex]t[/tex] é o número de triângulos construídos e [tex]p[/tex] é o número de palitos que utilizamos na construção, podemos concluir que:
- [tex]p=3\times1+2\times(t-1)[/tex].
Com essa informação, já podemos responder aos dois itens do problema.
a) Se [tex]t=2018[/tex], então:
[tex]\qquad p=3+2\times(2018-1)[/tex]
[tex]\qquad p=3+2\times2017[/tex]
[tex]\qquad p=3+4034[/tex]
[tex]\qquad p=4037[/tex].
Podemos, então, concluir que são necessários [tex] \, \fcolorbox{black}{#eee0e5}{$4.037$} \, [/tex] palitos para formar [tex]2.018[/tex] triângulos.
b) Se [tex]p=289[/tex], então:
[tex]\qquad 289=3+2\times(t-1)[/tex]
[tex]\qquad 289-3=2\times(t-1)[/tex]
[tex]\qquad 286=2\times(t-1)[/tex]
[tex]\qquad \dfrac{286}{2}=t-1[/tex]
[tex]\qquad 143=t-1[/tex]
[tex]\qquad 144=t[/tex].
Logo, teremos [tex] \, \fcolorbox{black}{#eee0e5}{$144$}[/tex] triângulos formados com [tex]289[/tex] palitos.
Solução elaborada pelos Moderadores do Blog.
