Problema
(Indicado a partir do 9º ano do E. F.)
(OBM) De um ponto qualquer marcado no interior de um triângulo equilátero, traçam-se segmentos perpendiculares a todos os lados. Demonstre que a soma dos comprimentos dos segmentos traçados é igual à altura do triângulo.
Solução
Considere o triângulo equilátero [tex]ABC[/tex] de lados com comprimento [tex]l[/tex] e altura com comprimento [tex]h.[/tex] Sejam [tex]d_1,\ d_2[/tex] e [tex]d_3[/tex] as medidas dos segmentos perpendiculares aos lados desse triângulo e traçados a partir de um ponto [tex]D[/tex], no seu interior.
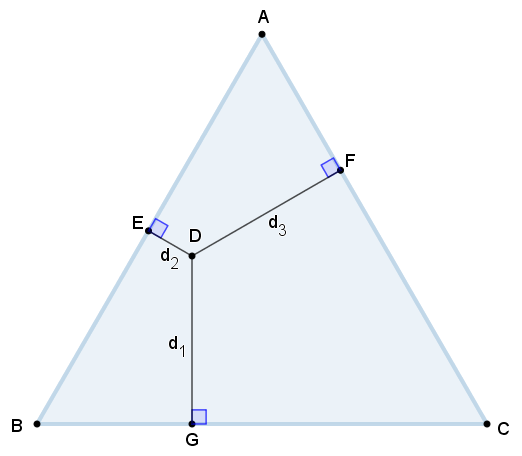
A área desse triângulo [tex]ABC[/tex] é dada por [tex]\dfrac{l\times h}{2}.[/tex]
Observe que essa área também pode ser vista como a soma das áreas dos triângulos [tex]ADB[/tex], [tex]BDC[/tex] e [tex]CDA[/tex].
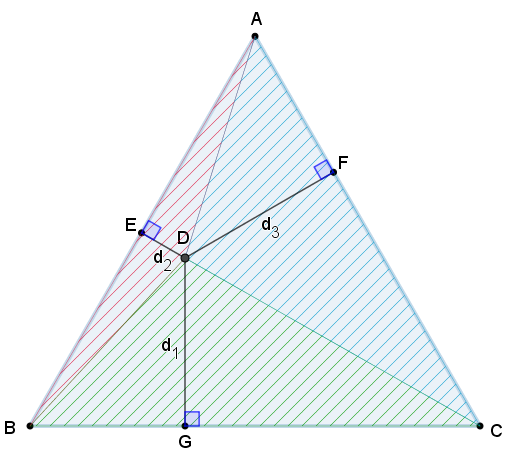
Podemos calcular as áreas de cada um desses três triângulos tomando os lados do triângulo [tex]ABC[/tex] como bases (todas, portanto, medindo [tex]l[/tex]) e os três segmentos perpendiculares aos lados como as respectivas alturas. Por exemplo, no triângulo [tex]ADB[/tex], o segmento [tex]AB[/tex], com comprimento [tex]l[/tex], é uma base e o segmento [tex]DE[/tex], com comprimento [tex]d_2[/tex], é uma altura; logo, sua área é [tex] \, \, \dfrac{l\times d_2}{2}[/tex].
Fazendo o mesmo para os outros triângulos, podemos concluir que:
[tex]\qquad \dfrac{l\times h}{2}=\dfrac{d_1\times l}{2}+\dfrac{d_2\times l}{2}+\dfrac{d_3\times l}{2}.\\[/tex]
Simplificando a igualdade obtida, obtemos [tex] \, \fcolorbox{black}{#eee0e5}{$d_1+d_2+d_3=h$} \, [/tex], como queríamos demonstrar.
Solução elaborada pelos Moderadores do Blog.
