Problema
(Indicado a partir do 3º ano do E. M.)
(Fundamentos de Matemática Elementar, Vol. 10 – Adaptado) Sejam [tex]P[/tex] e [tex]Q[/tex] pirâmides quadrangulares regulares tais que a base de [tex]P[/tex] é formada pelos pontos médios das arestas da base de [tex]Q[/tex]. Sabendo
- que o volume de [tex]Q[/tex] é [tex]48\; m^3[/tex],
- que o vértice de [tex]P[/tex] pertence à altura de [tex]Q[/tex]
- e que a distância deste vértice ao vértice de [tex]Q[/tex] é [tex]\frac{1}{3}[/tex] desta altura,
determine o volume da pirâmide [tex]P[/tex].
Solução
Na figura a seguir, ilustramos as pirâmides [tex]P[/tex] e [tex]Q[/tex], de acordo com as informações do problema.
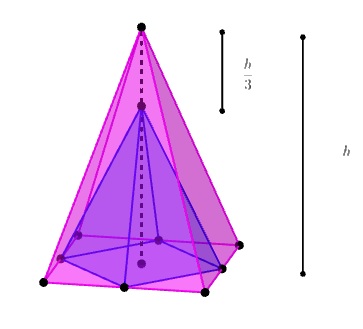
Vamos calcular o comprimento do lado da base da pirâmide [tex]P[/tex] usando a medida do lado da base da pirâmide [tex]Q[/tex]. Na figura abaixo, temos as bases das pirâmides [tex]Q[/tex] e [tex]P[/tex]. Sendo [tex] l[/tex] o comprimento do lado da base da pirâmide [tex]Q[/tex] podemos encontrar o comprimento [tex]a[/tex] do lado da base da pirâmide [tex]P.[/tex]
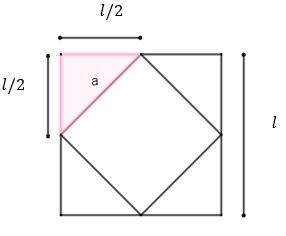
Notemos que o triângulo em destaque é retângulo, assim:
\begin{eqnarray}
a^2&=&\bigg(\frac{l}{2}\bigg)^2+\bigg(\frac{l}{2}\bigg)^2\\\nonumber
a^2&=&\frac{l^2}{4}+\frac{l^2}{4}\\ \nonumber
a^2&=&\frac{l^2}{2}\\
a&=&\frac{l\sqrt{2}}{2}.\;\;\;
\end{eqnarray}
Considere [tex]h[/tex] o comprimento da altura da pirâmide [tex]Q[/tex]. Assim, o comprimento da altura [tex]h_1[/tex] da pirâmide [tex] P[/tex] é [tex]h_1=\frac{2}{3}\cdot h[/tex]. Sabemos que o volume de uma pirâmide qualquer é [tex] V=\frac{1}{3}\cdot B\cdot h'[/tex], sendo [tex]B[/tex] a área da base e [tex]h'[/tex] o comprimento da sua altura. Logo, os volumes [tex] V_Q[/tex] e [tex] V_P[/tex] das pirâmides [tex]Q[/tex] e [tex]P[/tex], respectivamente, são dados por
\begin{eqnarray}\label{v2}
V_Q=\frac{1}{3}\cdot l^2\cdot h.\;\;\;\textcolor{#800000}{(i)}
\end{eqnarray}
\begin{eqnarray}
V_P=\frac{1}{3}\cdot \bigg(\frac{l\sqrt{2}}{2}\bigg)^2\cdot h_1.\;\;\;
\end{eqnarray}
Como o volume de [tex]Q[/tex] é [tex]48\; m^3[/tex], substituindo esse valor em [tex]\textcolor{#800000}{(i)}[/tex] e calculando [tex]h[/tex], temos que
\begin{eqnarray}\nonumber
\frac{1}{3}\cdot l^2 \cdot h=48\\
h=\frac{144}{l^2}.
\end{eqnarray}
Agora, podemos calcular o volume da pirâmide [tex]P[/tex]:
\begin{eqnarray}\nonumber
V_P=\frac{1}{3}\cdot\frac{l^2\cdot 2}{4}\cdot h_1\\ \nonumber
V_P=\frac{1}{3}\cdot\frac{l^2\cdot 2}{4}\cdot \frac{2}{3}\cdot\frac{144}{l^{2}}\\
\fcolorbox{black}{#eee0e5}{$V_P=16\;m^3$} \, .
\end{eqnarray}
Solução elaborada pelos Moderadores do Blog.
