Problema
(Indicado a partir do 7º ano do E. F.)
Explore a seção “Algoritmo de Euclides para determinação de MDC” que está disponibilizada na Ludoteca do Blog dos Clubes (mais precisamente em Aplicativos para estudar) e procure determinar todas as possibilidades para o número [tex]b[/tex], sabendo que [tex]mdc(4035, b)=5~[/tex] e que, para obtenção deste valor, o dispositivo prático utilizado foi o Algoritmo de Euclides para MDC, embora alguns números tenham desaparecido, como mostra a figura abaixo…

Solução
A ideia para resolução deste problema é atacá-lo de trás para frente.
Considerando, então, k o valor que aparece acima de 5 no diagrama inicial, teremos o preenchimento que segue.
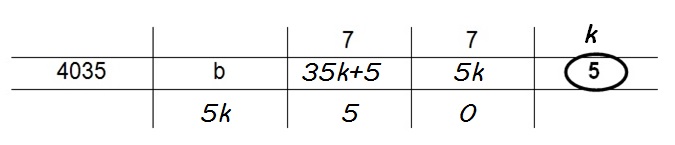
Nesse caso, concluiremos que
[tex]\qquad \qquad b = 7\times (35k+5)+5k = 250k+35[/tex],
o que nos dá as seguintes possibilidades para os valores de b (menores do que [tex]4035[/tex]):
[tex]\qquad \qquad 285, ~535, ~785, ~1035, ~1285, ~1535, ~1785, ~2035, ~2285, ~2535, ~2785,\\
\qquad \qquad 3035,~3285, ~3535 \text{ e }3785.[/tex]
Considerando, então, k o valor que aparece acima de 5 no diagrama inicial, teremos o preenchimento que segue.
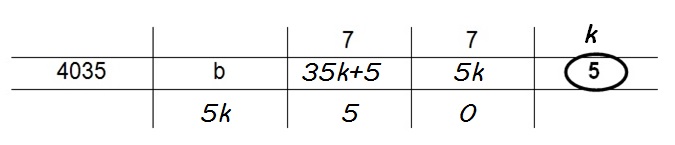
Nesse caso, concluiremos que
[tex]\qquad \qquad b = 7\times (35k+5)+5k = 250k+35[/tex],
o que nos dá as seguintes possibilidades para os valores de b (menores do que [tex]4035[/tex]):
[tex]\qquad \qquad 285, ~535, ~785, ~1035, ~1285, ~1535, ~1785, ~2035, ~2285, ~2535, ~2785,\\
\qquad \qquad 3035,~3285, ~3535 \text{ e }3785.[/tex]
- Como [tex]4035=3\cdot 5\cdot 269[/tex], vemos que b não pode ser múltiplo de 3 (nem de 269), pois nesse caso, o mdc (4035,b) seria maior do que 5.
Assim, podemos descartar os valores [tex]285, 1035, 1785, 2535[/tex] e [tex]3285[/tex] que visivelmente são múltiplos de 3, já que as respectivas soma de seus algarismos são múltiplos de 3. - Dos valores restantes,
[tex]\qquad 535, ~785, ~1285, ~1535, ~2035, ~2285, ~2785,~3035,~3535 \text{ e }3785[/tex],
os únicos que satisfazem a configuração apresentada para os respectivos dispositivos práticos utilizados no cálculo do MDC são [tex]785[/tex] e [tex]1285[/tex].
Por exemplo, veja que embora tenhamos [tex]mdc(4035, 2285)=5[/tex], o diagrama relativo ao cálculo não tem a configuração apresentada no enunciado do problema!
1 1 3 3 1 2 4 2 4035 2285 1750 535 145 100 45 10 5 1750 535 145 100 45 10 5 0
Então, os valores possíveis para b são [tex]785[/tex] e [tex]1285[/tex].
Você pode verificar a resposta utilizando a maquineta sugerida ou fazendo seus próprios cálculos com o ALGORITMO DE EUCLIDES!!!
Solução elaborada pelos Moderadores do Blog.
