Problema
(Indicado a partir do 9º ano do E. F.)
A planta baixa de uma casa popular está representada na figura a seguir.
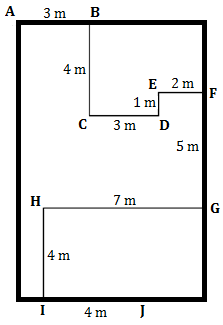
Cada segmento de reta que aparece na figura corresponde a uma parede e os pontos destacados estão todos a uma mesma altura de [tex]1,5[/tex] m em relação ao piso da casa. Sabe-se ainda que a distância do piso para a laje do teto é [tex]4[/tex] m.
Um eletricista deseja embutir nas paredes eletrodutos rígidos para a fiação elétrica e seguirá o caminho [tex]ABCDEFGHIJ[/tex], muito embora essa não seja a opção mais econômica. Para gastar a menor quantidade possível de eletroduto unindo os pontos [tex]A[/tex] e [tex]J[/tex], quantos metros do produto o eletricista utilizará?
Solução
Observemos, inicialmente, a planta da casa com todas as medidas indicadas.
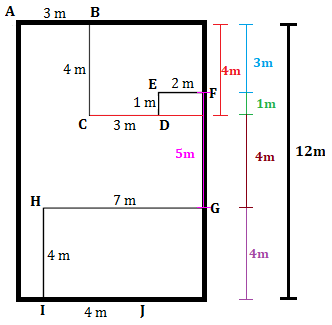
Para gastar a menor quantidade possível de eletroduto, parte do caminho de [tex]A[/tex] a [tex]J[/tex] deve ser feito sob o piso, pois esses dois pontos estão mais próximos do piso que da laje. Faremos duas planificações possíveis, [tex](I)[/tex] e [tex](II)[/tex], do piso e de parte das paredes onde estão os pontos [tex]A[/tex] e [tex]J[/tex].
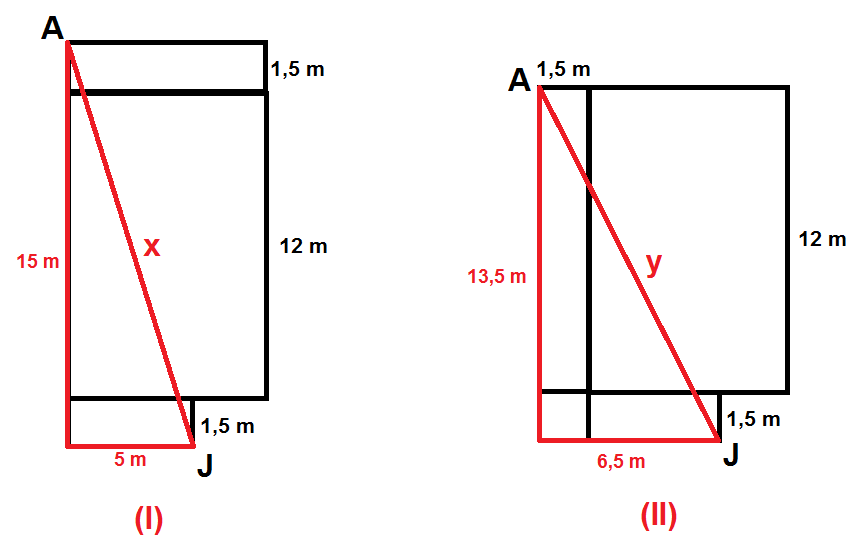
Na planificação [tex](I)[/tex], o valor de [tex]x[/tex] no triângulo retângulo de lados [tex]x[/tex], [tex]5[/tex] e [tex]15[/tex] corresponde a, aproximadamente, [tex]15,81\ m[/tex]. Na planificação [tex](II)[/tex], o valor de [tex]y[/tex] no triângulo retângulo de lados [tex]y[/tex], [tex]6,5[/tex] e [tex]13,5[/tex] corresponde a, aproximadamente, [tex]14,98\ m[/tex]. Portanto, a menor quantidade de eletroduto é, aproximadamente, [tex] \, \fcolorbox{black}{#eee0e5}{$15\ m$} \, .[/tex]
Existe uma solução intuitiva (e bastante utilizada na prática) que, para unir os pontos [tex]A[/tex] e [tex]J[/tex] com eletrodutos, poderia ser descrita pelo seguinte caminho:
- a partir do ponto [tex]J[/tex], desce o eletroduto perpendicularmente até o chão, ponto [tex]J'[/tex];
- a partir do ponto [tex]A[/tex], desce o eletroduto perpendicularmente até o chão, ponto [tex]A'[/tex];
- une os pontos [tex]A'[/tex] e [tex]J'[/tex].
Vejam a planificação abaixo; ela nos mostra a quantidade de eletrodutos a ser utilizada, em metros.
São gastos:
- [tex]1,5 \, m[/tex] de [tex]A[/tex] até [tex]A'[/tex];
- [tex]1,5 \, m[/tex] de [tex]J[/tex] até [tex]J'[/tex];
- a distância entre os pontos [tex]A'[/tex] e [tex]J'[/tex] é o comprimento [tex]l[/tex] da hipotenusa de um triângulo retângulo de catetos com comprimentos [tex]5 \, m[/tex] e [tex]12 \, m[/tex]:
[tex]\quad l^2=12^2+5^2\\
\quad l^2=169\\
\quad l=\pm 13\\
\quad l=13 \, m \text{, pois l}\gt 0.[/tex]
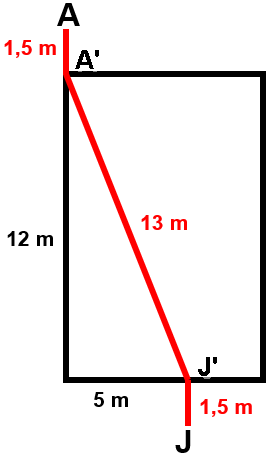
Assim, com o caminho [tex]AA’J’J[/tex] seriam gastos [tex]1,5+1,5+13=16 \, m \, [/tex] de eletrodutos; mais do que cada uma das duas situações anteriormente apresentadas.
Nas planificações [tex](I)[/tex] e [tex](II)[/tex], vamos acrescentar esse novo caminho, em azul, para apresentarmos uma justificativa visual da afirmação de que os dois caminhos anteriores são mais econômicos que o terceiro.
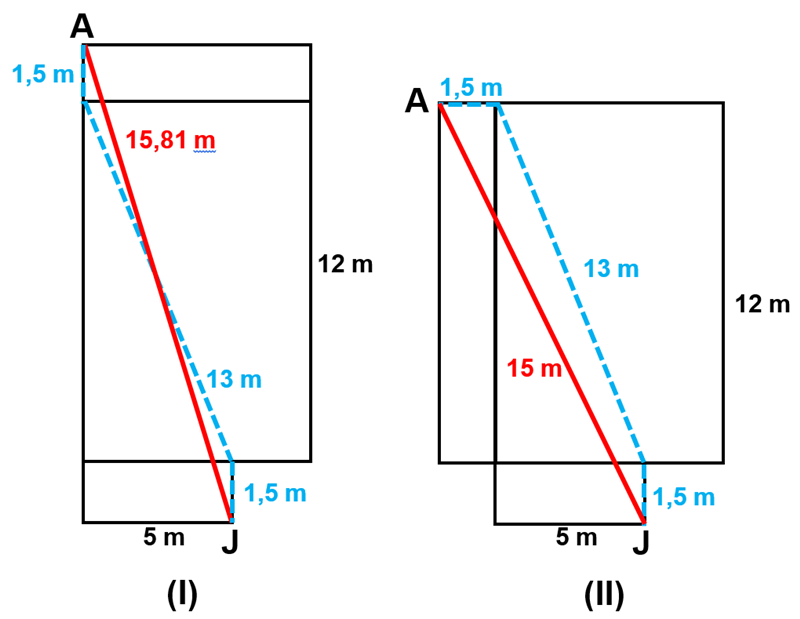
Nas duas situações, é só lembrar que "a menor distância entre dois pontos é definida pelo segmento que os une".
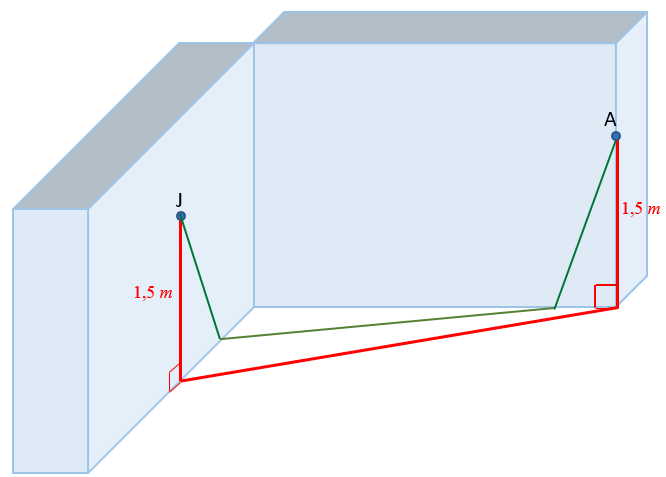
Saindo do plano, a última imagem ilustra o caminho da planificação [tex](II)[/tex] e o último caminho apresentado.
Solução elaborada pelos Moderadores do Blog.
