Problema
(Indicado a partir do 2º ano do E. M.)
(UNIUBE 2001 – Adaptado) O código Morse é um sistema de transmissão de informações em que as letras do alfabeto, numerais, etc., são representados por conjuntos ordenados de pontos e traços. Exemplos:
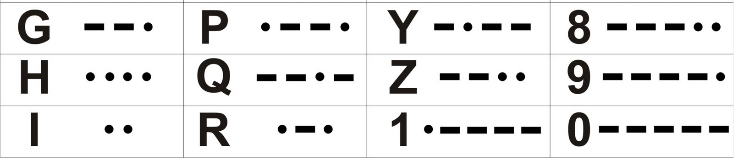
Assim, para representar a letra [tex]G[/tex] precisamos de um conjunto ordenado de comprimento [tex]3[/tex], pois utilizamos [tex]2[/tex] traços e [tex]1[/tex] ponto. Já no caso do [tex]9[/tex], o conjunto ordenado tem comprimento [tex]5[/tex], pois utilizamos [tex]4[/tex] traços e [tex]1[/tex] ponto.
Sabendo que as letras são codificadas com os conjuntos de menores comprimentos possíveis e considerando o nosso alfabeto composto por [tex]26[/tex] letras, para fazer a codificação de todas essas letras, qual o comprimento máximo dos conjuntos ordenados utilizados?
Solução
Observemos que, para um certo comprimento, há duas opções para cada símbolo (ponto ou traço). Dessa forma, pelo Princípio Fundamental da Contagem, temos que:
► com [tex]1[/tex] elemento, podemos escrever até: [tex]2^1 = 2[/tex] letras;
► com [tex]2[/tex] elementos, podemos escrever até: [tex]2^2 = 4[/tex] letras;
► com [tex]3[/tex] elementos, podemos escrever até: [tex]2^3 = 8[/tex] letras;
► com [tex]4[/tex] elementos, podemos escrever até: [tex]2^4 = 16[/tex] letras.
Desse modo, como [tex]2 + 4 + 8 + 16 = 30[/tex], podemos, com comprimento máximo [tex] \, \fcolorbox{black}{#eee0e5}{$4$} \, [/tex], codificar todas as [tex]26[/tex] letras do alfabeto.
Observe que não é possível codificar as [tex]26[/tex] letras com comprimento máximo [tex]3[/tex], visto que [tex]2 + 4 + 8 = 14.[/tex]
Solução elaborada pelos Moderadores do Blog.
