Problema
(Indicado a partir do 6º ano do E. F.)
Lúcia notou que cada número da sequência [tex]1 \, , \, 3 \, , \, 6 \, , \, 10 \, , \, \cdots [/tex] pode ser modelado por meio de um conjunto de bolinhas que, dispostas convenientemente, formam um triângulo, conforme ilustra a figura mostrada abaixo.
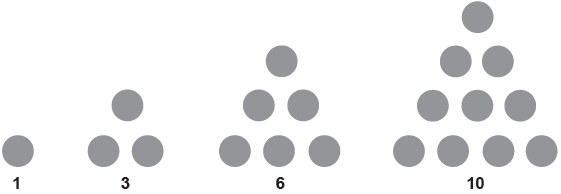
Seguindo o mesmo padrão, quantas bolinhas terá o triângulo associado ao décimo termo dessa sequência numérica?
Solução 1
A partir da construção dos triângulos, percebemos que a sequência numérica observada por Lúcia pode ser assim definida:
[tex]\qquad 1^\circ[/tex] termo: [tex]1[/tex];
[tex]\qquad 2^\circ [/tex] termo: [tex]1 + 2 = 3[/tex];
[tex]\qquad 3^\circ [/tex] termo: [tex]1 + 2 + 3 = 6[/tex];
[tex]\qquad 4^\circ [/tex] termo: [tex]1 + 2 + 3 + 4 = 10[/tex];
[tex]\qquad 5^\circ [/tex] termo: [tex]1 + 2 + 3 + 4 + 5 = 15[/tex];
[tex]\qquad 6^\circ [/tex] termo: [tex]1 + 2 + 3 + 4 + 5 + 6 = 21[/tex];
[tex]\qquad 7^\circ [/tex] termo: [tex]1 + 2 + 3 + 4 + 5 + 6 + 7 = 28[/tex];
[tex]\qquad 8^\circ [/tex] termo: [tex]1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = 36[/tex];
[tex]\qquad 9^\circ [/tex] termo: [tex]1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45[/tex];
[tex]\qquad 10^\circ [/tex] termo: [tex]1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = 55.[/tex]
Dessa forma, a representação do décimo termo da sequência tem [tex]55[/tex] bolinhas e, portanto, o décimo termo da sequência é exatamente o [tex] \, \fcolorbox{black}{#eee0e5}{$ \, 55 \, $} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
Solução 2
O décimo termo da sequência em questão terá [tex]55[/tex] bolinhas; pois, se seguirmos a sequência, descobriremos que a base do décimo termo corresponde ao número de [tex]10[/tex] bolinhas, sendo que se forma um triângulo no qual em cada carreira será diminuída uma bolinha.
Portanto:
[tex]\qquad 10+9+8+7+6+5+4+3+2+1= 55[/tex] bolinhas no total.
Solução elaborada pelo COM OCTETO MATEMÁTICO, com contribuições dos Moderadores do Blog.

Para aprender mais
A soma dos números naturais de [tex]1[/tex] até [tex]n[/tex] é chamada termial de [tex]n[/tex] e representada por [tex]\boxed{n?}[/tex](É com o ponto de interrogação mesmo, viu?). Assim, sendo [tex]n\in\mathbb{N}[/tex], temos [tex]n?=n+(n-1)+(n-2)+\ldots+1[/tex].
Dessa forma, poderíamos responder que o décimo termo da sequência de Lúcia é [tex] \, \fcolorbox{black}{#eee0e5}{$ \, 10?$}.[/tex]
Uma maneira mais rápida de se calcular esta soma pode ser aprendida na Sala de Estudo A soma [tex]1 + 2 + 3 +\ldots + t[/tex].
