Problema
(Indicado a partir do 9º ano do E. F.)
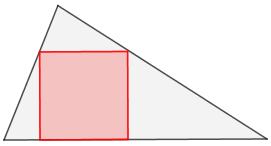
Descobrir um método geométrico para inscrever um quadrado num dado triângulo qualquer.
Um dos lados do quadrado deve estar sobre o maior lado do triângulo e os outros dois vértices do quadrado devem ficar sobre os outros dois lados do triângulo, como na figura abaixo.

Lembretes e notações
(1) Caso de Semelhança A.A. (ângulo – ângulo): Se dois ângulos de um triângulo são congruentes a dois ângulos de outro triângulo, então estes triângulos são semelhantes.
(2) Em triângulos semelhantes, os lados correspondentes são proporcionais.
(Há uma Sala de Ajuda sobre triângulos semelhantes no nosso Blog!)
(3) Denotaremos o segmento definido por dois pontos, digamos [tex]X[/tex] e [tex]Y[/tex], por [tex]\overline{XY}[/tex] e o comprimento desse segmento por [tex]XY[/tex].
(4) Denotaremos o ângulo de vértice [tex]V[/tex] e definido por dois pontos, digamos [tex]X [/tex] e [tex]Y[/tex], por [tex]X\widehat{V}Y. [/tex]
Solução 1
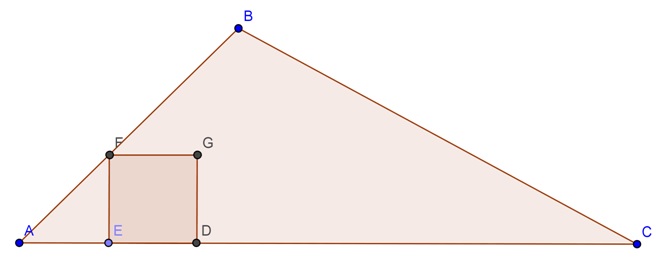
Inicialmente, no triângulo [tex]ABC[/tex] dado (consideremos [tex]\overline{AC}[/tex] o maior lado), construímos um quadrado que tenha dois de seus vértices sobre [tex]\overline{AC}[/tex] e um vértice sobre [tex]\overline{AB}[/tex], como ilustra a figura abaixo. Seja [tex]G[/tex] o quarto vértice do quadrado (observamos que este vértice poderia estar no exterior do triângulo).
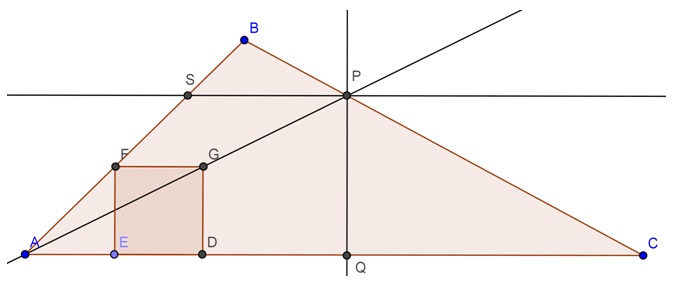
Feito isto, traçamos a reta [tex]AG[/tex] e definimos o ponto [tex]P[/tex], intersecção da reta [tex]AG[/tex] e [tex]\overline{BC}[/tex]. A partir de [tex]P[/tex], traçamos uma reta paralela à reta [tex]AC[/tex] e uma perpendicular à reta [tex]AC[/tex], definindo assim os pontos de interseção [tex]S[/tex] e [tex]Q[/tex], respectivamente (como ilustra a figura abaixo).
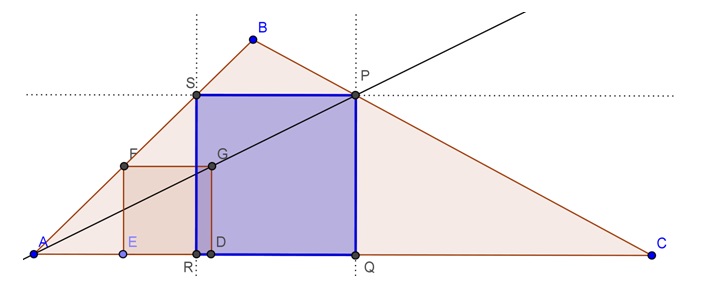
Finalmente, com uma perpendicular à reta [tex]AC[/tex] passando por [tex]S[/tex], teremos o ponto [tex]R[/tex], intersecção da reta [tex]AC[/tex] com a perpendicular traçada. O quadrilátero [tex]PQRS[/tex] é a solução do problema.
Por que a solução é boa?
- Reparem que, pela construção feita, os triângulos [tex]APQ[/tex] e [tex]AGD[/tex] são semelhantes, já que os ângulos [tex]P\widehat{Q}A[/tex] e [tex]G\widehat{D}A[/tex] têm a mesma medida (ambos são ângulos retos) e [tex]P\widehat{A}C[/tex] é um ângulo comum aos dois triângulos. Assim, [tex]\dfrac{PQ}{AP} = \dfrac{GD}{AG}[/tex].
Os triângulos [tex]AFG[/tex] e [tex]ASP[/tex] também são semelhantes (Que tal você verificar?); assim, da mesma forma, temos que [tex]\dfrac{SP}{AP} = \dfrac{FG}{AG}[/tex].
Como [tex]\overline{GD}[/tex] e [tex]\overline{FG}[/tex] são lados de um mesmo quadrado, então [tex]GD=FG[/tex] e, portanto, concluímos que [tex]SP= PQ[/tex]. - Os ângulos retos do quadrilátero [tex]PQRS[/tex] podem ser verificados por construção e por paralelismo.
Sendo assim, temos que [tex]PQRS[/tex] é, de fato, um quadrado, respeitando-se as condições estabelecidas pelo problema.
Solução elaborada pelos Moderadores do Blog.
Solução 2
Utilizando o mesmo triângulo [tex]ABC[/tex] apresentado na solução anterior, construímos o quadrado [tex]ACDE[/tex] sobre o lado [tex]\overline{AC}[/tex] (no semiplano oposto ao do triângulo inicial) e traçamos as retas [tex]BD[/tex] e [tex]BE[/tex], como ilustra a figura abaixo.
Pelos pontos de intersecção das retas [tex]BD[/tex] e [tex]BE[/tex] com [tex]\overline{AC}[/tex] ([tex]Q[/tex] e [tex]R[/tex], respectivamente), traçamos as perpendiculares à reta [tex]AC[/tex], que definirão, respectivamente, os pontos [tex]P[/tex] e [tex]S[/tex].
Assim, teremos que o quadrilátero [tex]PQRS[/tex] define o quadrado que é solução do problema.
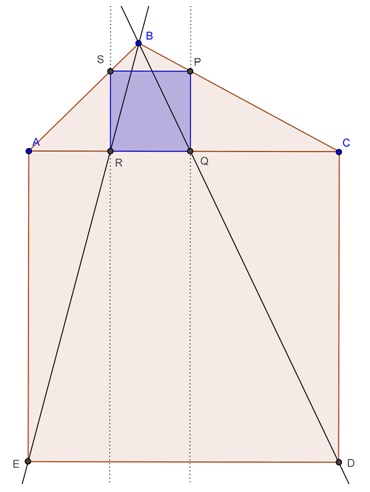
Deixamos para que você verifique por que esta solução também é correta. Como sugestão, vocês podem analisar três pares de triângulos:
- triângulo [tex]BSR[/tex] e triângulo [tex]BAE[/tex],
- triângulo [tex]BPQ[/tex] e triângulo [tex]BCD[/tex],
- triângulo [tex]BQR[/tex] e triângulo [tex]BDE[/tex].
Solução elaborada pelos Moderadores do Blog.
