Problema
(Indicado a partir do 2º ano do E. M.)
(Problema adaptado de Olimpíada Americana) Um cilindro circular reto de isopor com raio da base medindo [tex]2\ cm[/tex] e altura [tex]2 \sqrt{2}\ cm[/tex] foi seccionado por um plano que o dividiu ao meio de forma que os pontos [tex]A[/tex] e [tex]B[/tex] foram marcados na circunferência de uma das bases e os pontos [tex]C[/tex] e [tex]D[/tex] foram marcados na face oposta conforme figura. Sabe-se que o arco menor que passa por [tex]A[/tex] e [tex]B[/tex] é de [tex]120^\circ[/tex] (ver figura), bem como o arco menor que passa por [tex]C[/tex] e [tex]D[/tex].
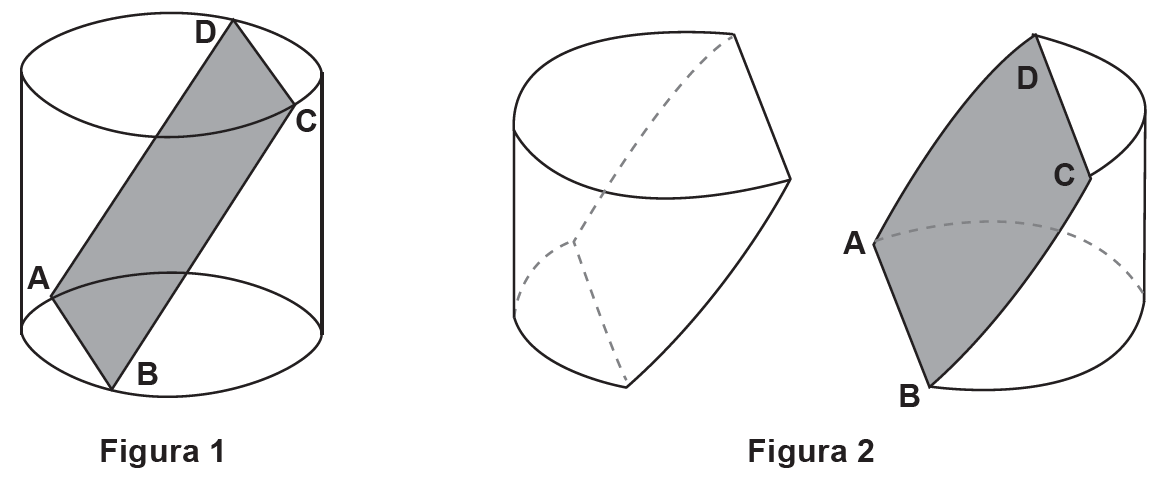
Determine a área do retângulo formado na secção do cilindro quando ligamos os pontos [tex]A[/tex], [tex]B[/tex], [tex]C[/tex], [tex]D[/tex] por segmentos de reta.
Solução
[tex]\textcolor{#800000}{(1)}[/tex] Inicialmente, vamos calcular a medida do lado [tex]AB[/tex] do retângulo [tex]ABCD[/tex]. Para isso, seja [tex]O[/tex] o centro da circunferência na qual os pontos [tex]A[/tex] e [tex]B[/tex] foram marcados, conforme mostra a figura a seguir.
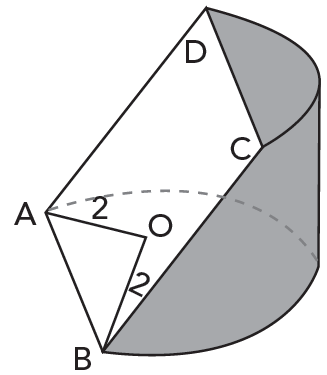
Aplicando a Lei dos Cossenos no triângulo [tex]AOB[/tex] e sabendo que o arco menor que passa por [tex]A[/tex] e [tex]B[/tex] é de [tex]120^\circ[/tex], vem que:
[tex]\qquad (AB)^2=2^2+2^2-2\cdot 2 \cdot 2 \cdot cos 120^\circ [/tex]
[tex]\qquad (AB)^2=8-8\cdot \left(-\dfrac{1}{2}\right) [/tex]
[tex]\qquad (AB)^2=12[/tex]
[tex]\qquad \fcolorbox{black}{#e8e8e8}{$AB=2\sqrt{3} \, cm$} \, ,[/tex] uma vez que a medida do segmento [tex]AB[/tex] é positiva.
[tex]\textcolor{#800000}{(2)}[/tex] Para determinar a medida do lado [tex]BC[/tex] do retângulo [tex]ABCD[/tex], tomemos [tex]C’[/tex] e [tex]D’[/tex], projeções de [tex]C[/tex] e [tex]D[/tex], respectivamente, sobre a circunferência que contém [tex]A[/tex] e [tex]B[/tex].
Observe a figura abaixo e perceba que, como o arco menor que passa por [tex]A[/tex] e [tex]B[/tex] é de [tex]120^\circ[/tex], o ângulo [tex]B\hat{O}A[/tex] mede [tex]120^\circ[/tex] e, com isso, a medida em graus do ângulo [tex]B\hat{O}C'[/tex] é dada por [tex]\boxed{180^\circ-120^\circ=60^\circ}.[/tex]
Como [tex]OB=OC’=2[/tex] e a medida de [tex]B\hat{O}C'[/tex] é [tex]60^\circ[/tex], o triângulo [tex]OBC’[/tex] é equilátero de lado [tex]2[/tex].
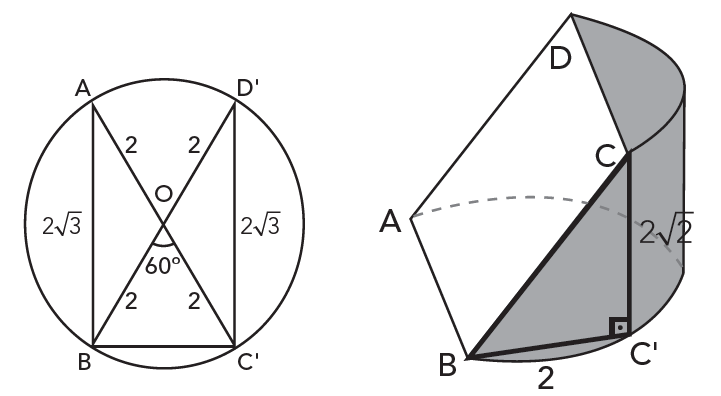
A medida de [tex]BC[/tex] é obtida utilizando-se o Teorema de Pitágoras no triângulo [tex]BCC’[/tex]. Veja:
[tex]\qquad (BC)^2=2^2+(2\sqrt{2})^2[/tex]
[tex]\qquad (BC)^2=4+8 [/tex]
[tex]\qquad (BC)^2=12 [/tex]
[tex]\qquad \fcolorbox{black}{#e8e8e8}{$(BC)=2\sqrt{3}\ cm$} \, .[/tex]
Finalmente, a área do retângulo [tex]ABCD[/tex] é [tex] \, \fcolorbox{black}{#eee0e5}{$(AB)\cdot(BC)=2\sqrt{3} \cdot 2\sqrt{3}=12 \, cm^2$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
