Problema
(Indicado a partir do 9º ano do E. F.)
Dois lados consecutivos de um quadrilátero circunscrito a um círculo medem [tex]7\ cm[/tex] e [tex]5\ cm[/tex]. Calcule a medida dos outros dois lados sabendo que o perímetro mede [tex]26\ cm[/tex].

Lembrete
Para solução deste problema, utilizaremos a seguinte propriedade de tangentes a uma circunferência:
- Se de um ponto [tex]P[/tex] conduzirmos os segmentos [tex]\overline{PG}[/tex] e [tex]\overline{PH}[/tex] tangentes a uma circunferência, sendo [tex]G[/tex] e [tex]H[/tex] pontos da circunferência, então [tex]\overline{PG}[/tex] e [tex]\overline{PH}[/tex] têm o mesmo comprimento.
Solução
Para acompanhar o nosso raciocínio, observe o quadrilátero [tex]ABCD[/tex] abaixo, circunscrito a um círculo.
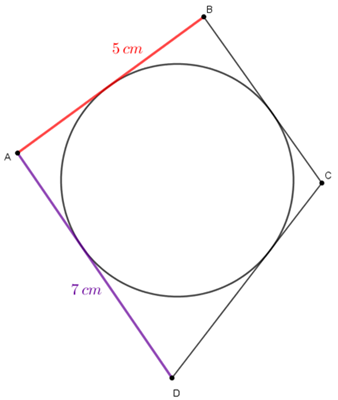
Considere que [tex]R \, [/tex] e [tex]S \, [/tex] são os pontos de tangência definidos respectivamente pelos segmentos [tex]\overline{AB} \, [/tex] e [tex] \, \overline{AD} \, .[/tex] Utilizando a propriedade do Lembrete, os segmentos [tex]\overline{AR} \, [/tex] e [tex] \, \overline{AS} \, [/tex] têm o mesmo comprimento, digamos [tex]x \, [/tex] centímetros, conforme ilustra a próxima figura.
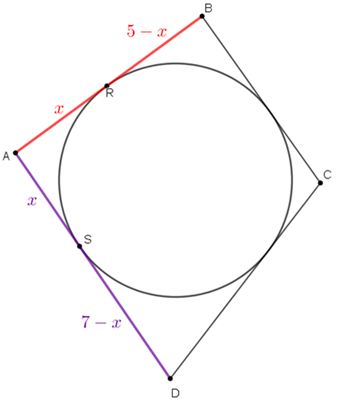
Utilizando a mesma propriedade citada no Lembrete, se [tex]U \, [/tex] e [tex]V \, [/tex] são respectivamente os pontos de tangência definidos pelos segmentos [tex]\overline{CB} \, [/tex] e [tex] \, \overline{CD} \, [/tex], então já temos os comprimentos dos segmentos [tex]\overline{BU} \, [/tex] e [tex] \, \overline{DV} \, [/tex], conforme mostra a próxima figura.
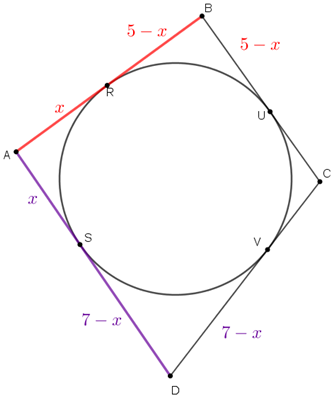
Usando a propriedade do Lembrete, mais uma vez, os segmentos [tex]\overline{UC} \, [/tex] e [tex] \, \overline{VC} \, [/tex] têm o mesmo comprimento, digamos [tex]a \, [/tex] centímetros.
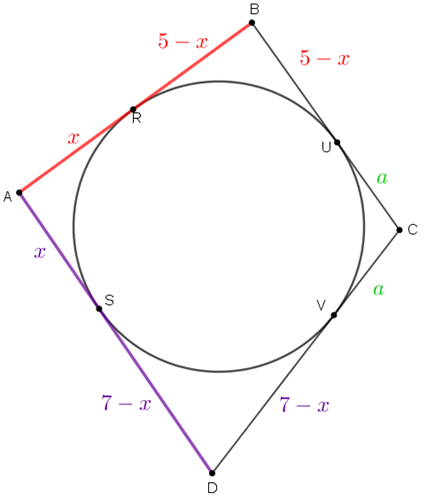
Sabemos que o perímetro do quadrilátero é [tex]26 \, cm[/tex], assim:
[tex]\qquad 5+7+(7-x+a)+(a+5-x)=26[/tex],
donde [tex] 2a-2x=2[/tex], ou ainda, [tex]\, a-x=1[/tex].
Como os valores das medidas dos lados que queremos descobrir são dados por [tex]\boxed{l_1=7-x+a} \, \, [/tex] e [tex] \, \, \boxed{l_2=5-x+a}[/tex] tem-se que:
[tex]\qquad \qquad \, \fcolorbox{black}{#eee0e5}{$l_1=7+a-x=7+1=8 \, cm$} \, \qquad [/tex] e [tex]\qquad \, \fcolorbox{black}{#eee0e5}{$l_2=5+a-x=5+1=6 \, cm$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
